Prismas

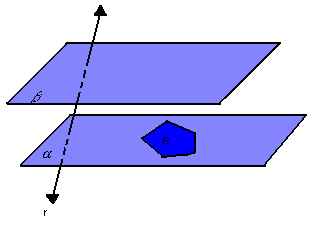
Na figura abaixo, temos dois planos paralelos e distintos, , um polígono convexo R contido em e uma reta r que intercepta , mas não R:

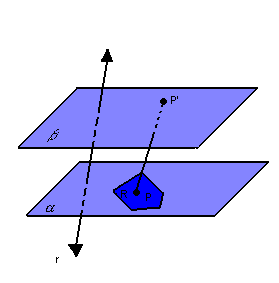
Para cada ponto P da região R, vamos considerar o segmento , paralelo à reta r :

      Assim, temos:

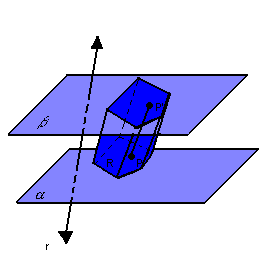
Chamamos de prisma ou prisma limitado o conjunto de todos os segmentos congruentes paralelos a r.

Elementos do prisma

Dado o prisma a seguir, consideramos os seguintes elementos:

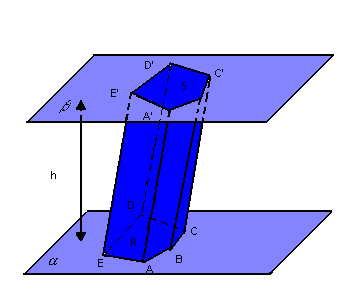
• bases: as regiões poligonais R e S

• altura: a distância h entre os planos

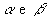
• arestas das bases: os lados 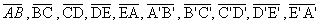( dos polígonos)

• arestas laterais: os segmentos

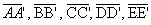
• faces laterais: os paralelogramos AA'BB', BB'C'C, CC'D'D, DD'E'E, EE'A'A.