Tronco de pirâmide

Se um plano interceptar todas as arestas de uma pirâmide, paralelamente às suas bases, dividirá o sólido em dois outros: uma nova pirâmide e um tronco de pirâmide. Dado o tronco de pirâmide regular a seguir, temos:

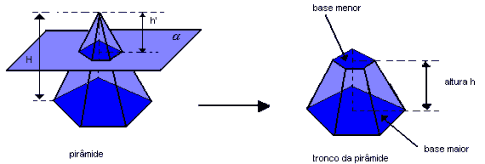
• as bases são polígonos regulares paralelos e semelhantes;

• as faces laterais são trapézios isósceles congruentes.

Áreas

Temos as seguintes áreas:

a) área lateral (A_L): soma das áreas dos trapézios isósceles congruentes que formam as faces laterais.

b) área total (A_T): soma da área lateral com a soma das áreas da base menor (A_b) e maior (A_B).

Volume

O volume de um tronco de pirâmide regular é dado por:

Sendo V o volume da pirâmide e V' o volume da pirâmide obtido pela secção, é válida a relação: