Paralelepípedo

Todo prisma cujas bases são paralelogramos recebe o nome de paralelepípedo. Assim, podemos ter:

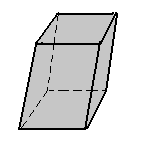
a) paralelepípedo oblíquo

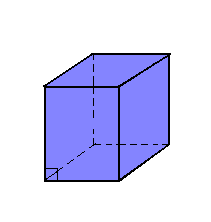
b) paralelepípedo reto

Se o paralelepípedo  reto tem bases retangulares, ele é chamado de paralelepípedo reto-retângulo, ortoedro ou paralelepípedo retângulo.

Paralelepípedo retângulo

Seja o paralelepípedo retângulo de dimensões a, b e c da figura:

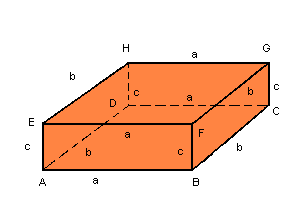
Temos quatro arestas de medida a, quatro arestas de medida b e quatro arestas de medida c; as arestas indicadas pela mesma letra são paralelas.

Diagonais da base e do paralelepípedo

Considere a figura a seguir:

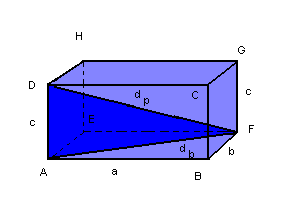
d_b = diagonal da base

d_p = diagonal do paralelepípedo

Na base ABFE, temos:

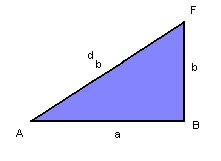
No triângulo AFD, temos:

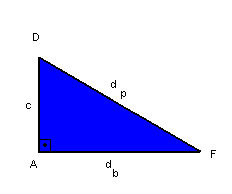
Área lateral

Sendo A_L a área lateral de um paralelepípedo retângulo, temos:

A_L= ac + bc + ac + bc
A_L= 2ac + 2bc
A_L = 2(ac + bc)

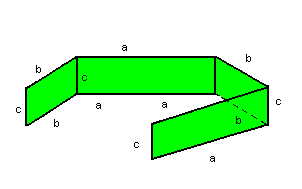
Área total

Planificando o paralelepípedo, verificamos que a área total é a soma das áreas de cada par de faces opostas:

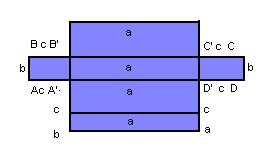
A_T= 2( ab + ac + bc)

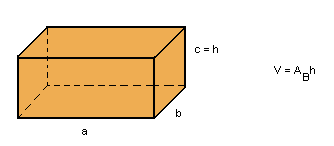
Volume

Por definição, unidade de volume é um cubo de aresta 1. Assim, considerando um paralelepípedo de dimensões 4, 2 e 2, podemos decompô-lo em 4 . 2 . 2 cubos de aresta 1:

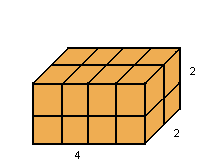
Então, o volume de um paralelepípedo retângulo de dimensões a, b e c é dado por:

V = abc

Como o produto de duas dimensões resulta sempre na área de uma face e como qualquer face pode ser considerada como base, podemos dizer que o volume do paralelepípedo retângulo é o produto da área da base A_B pela medida da altura h: