Laifis em destaque

Mitologia Grega 35 postagens Anatomia óssea 90 postagens

Filmes do Quentin Tarantino 24 postagens Barbie 85 postagens

Geometria Espacial
   

Secção paralela à base de uma pirâmide

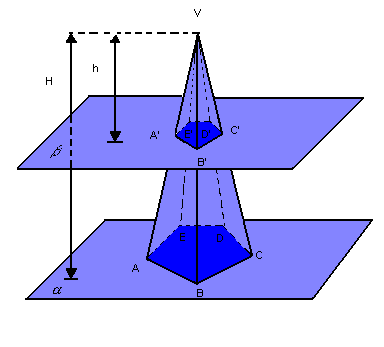
        Um plano paralelo à base que intercepte todas as arestas laterais determina uma secção poligonal de modo que:

• as arestas laterais e a altura sejam divididas na mesma razão;
• a secção obtida e a base sejam polígonos semelhantes;
• as áreas desses polígonos estejam entre si assim como os quadrados de suas distâncias ao vértice.

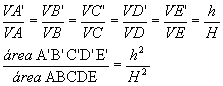
Relações entre os elementos de uma pirâmide regular

      Vamos considerar uma pirâmide regular hexagonal, de aresta lateral l e aresta da base a:

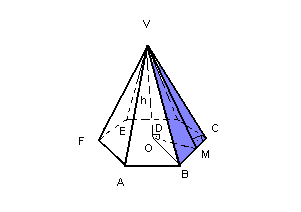
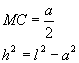
    Assim, temos:

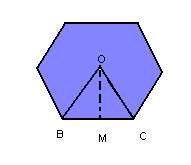
•  A base da pirâmide é um polígono regular inscritível em um círculo de raio OB = R.

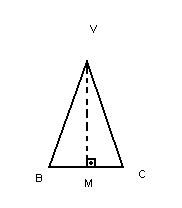
• A face lateral da pirâmide é um triângulo isósceles.

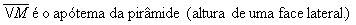
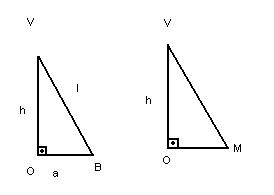
• Os triângulos VOB e VOM são retângulos.

<< Voltar para seção Ensino médio