📄 Axiomas
📄 Posições relativas de duas retas
📄 Determinação de um plano
📄 Posições relativas de reta e plano
📄 Perpendicularismo entre reta e plano
📄 Posições relativas de dois planos
📄 Projeção ortogonal
📄 Distâncias entre ponto, reta e planos
📄 Ângulos entre retas e planos
📄 Diedros, triedos, poliedros
📄 Poliedros
📄 Poliedros regulares
📄 Prismas
📄 Classificação dos prismas
📄 Secção do prisma
📄 Paralelepípedo
📄 Cubo
📄 Generalização do volume de um prisma
📄 Cilindro
📄 Secções do cilindro
📄 Área e volume do cilindro
📄 Cilindro equilátero
📄 Cone circular
📄 Área e volume do cone
📄 Pirâmide
📄 Secção paralela à base de uma pirâmide
📄 Área e volume da pirâmide
📄 Tronco de pirâmide
📄 Tronco de cone
📄 Esfera
📄 Partes da esfera
Cone circular
Dado um
círculo C, contido num plano 
,
e um ponto V (vértice) fora de ,
chamamos de cone circular o conjunto de todos os segmentos 
.
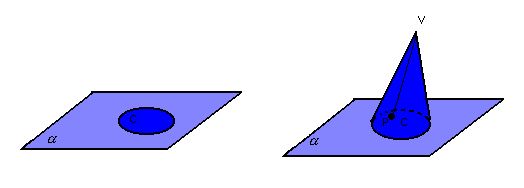
Elementos do cone circular
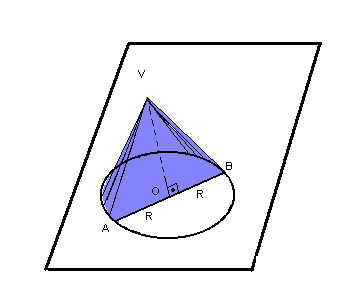
Dado o cone a seguir, consideramos os seguintes elementos:
-
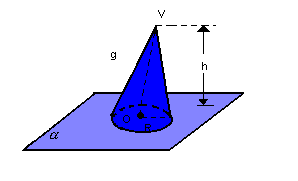
altura: distância h do vértice V ao plano
. -
geratriz (g): segmento com uma extremidade no ponto V e outra num ponto da circunferência.
-
raio da base: raio R do círculo.
-
eixo de rotação: reta
determinada
pelo centro do círculo e pelo vértice do cone.
Cone reto
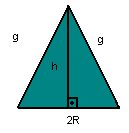
Todo cone cujo eixo de rotação é perpendicular à base é chamado cone reto, também denominado cone de revolução. Ele pode ser gerado pela rotação completa de um triângulo retângulo em torno de um de seus catetos.
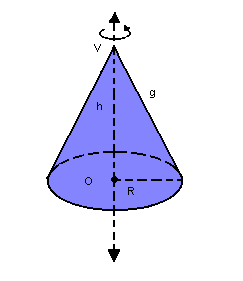
Da figura, e pelo Teorema de Pitágoras, temos a seguinte relação:
| g2 = h2 + R2 |
Secção meridiana
A secção determinada, num cone de revolução, por um plano que contém o eixo de rotação é chamada secção meridiana.
Se o triângulo AVB for equilátero, o cone também será equilátero:
