Área do cilindro

Em um cilindro, consideramos as seguintes áreas:

a) área lateral (A_L)

Podemos observar a área lateral de um cilindro fazendo a sua planificação:

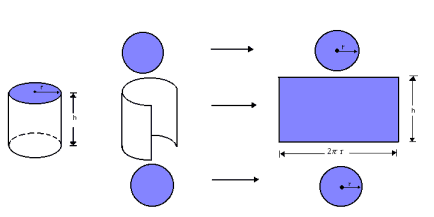
Assim, a área lateral do cilindro reto cuja altura é h e cujos raios dos círculos das bases são r é um retângulo de dimensões :

b) área da base (A_B): área do círculo de raio r.

c) área total (A_T): soma da área lateral com as áreas das bases.

Volume do cilindro

Para obter o volume do cilindro, vamos usar novamente o princípio de Cavalieri. Dados dois sólidos com mesma altura e um plano , se todo plano , paralelo ao plano , intercepta os sólidos e determina secções de mesma área, os sólidos têm volumes iguais:

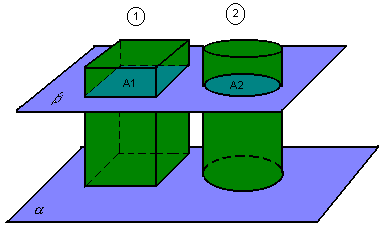
Se 1 é um paralelepípedo retângulo, então V₂ = A_Bh. Assim, o volume de todo paralelepípedo retângulo e de todo cilindro é o produto da área da base pela medida de sua altura:

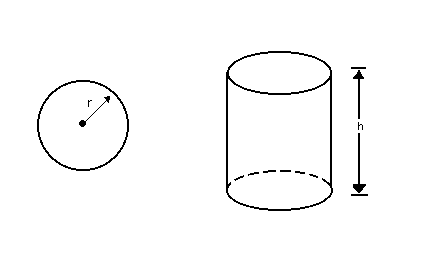
No caso do cilindro circular reto, a área da base é a área do círculo de raio r: . Portanto, seu volume é: