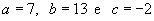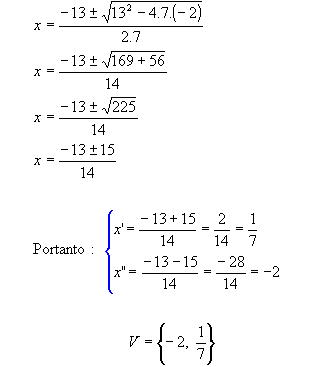📄 Raízes de uma equação do 2º grau
📄 Resolução de equações incompletas
📄 Resolução de equações completas
📄 Discriminante
📄 Equações literais
📄 Relações entre os coeficientes e as raízes
📄 Composição de uma equação de 2º grau
📄 Forma fatorada
📄 Equações biquadradas
📄 Resolução de uma equação biquadrada
📄 Composição da equação biquadrada
📄 Equações irracionais
📄 Sistemas de equações do 2º grau
📄 Problemas do 2º grau
📄 Outros exemplos
Resolução de equações completas
Para solucionar
equações completas do 2º grau utilizaremos a fórmula de Bhaskara. A partir da equação ![]() ,
em que a, b,
c
,
em que a, b,
c ![]() IR e
IR e ![]() ,
desenvolveremos passo a passo a dedução da fórmula de Bhaskara (ou fórmula
resolutiva).
,
desenvolveremos passo a passo a dedução da fórmula de Bhaskara (ou fórmula
resolutiva).
|
1º passo: multiplicaremos ambos os membros por 4a. |
![]()
|
2º passo: passar 4ac par o 2º membro. |
![]()
|
3º passo:
adicionar |
![]()
|
4º passo: fatorar o 1º elemento. |
![]()
|
5º passo: extrair a raiz quadrada dois membros. |
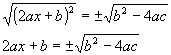
|
6º passo: passar b para o 2º membro. |
![]()
|
7º
passo: dividir os dois membros por |
![]()
Assim, encontramos a fórmula resolutiva da equação do 2º grau:
|
|
Podemos
representar as duas raízes reais por x' e x", assim:
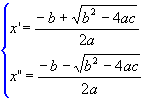
Exemplos:
-
Resolução da equação:
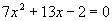 .
.
Temos