Equações irracionais

Considere as seguintes equações:

Observe que todas elas apresentam variável ou incógnita no radicando. Essas equações são irracionais. Ou seja:     

Resolução de uma equação irracional

A resolução de uma equação irracional deve ser efetuada procurando transformá-la inicialmente numa equação racional, obtida ao elevarmos ambos os membros da equação a uma potência conveniente.

Em seguida, resolvemos a equação racional encontrada e, finalmente, verificamos se as raízes da equação racional obtidas podem ou não ser aceitas como raízes da equação irracional dada (verificar a igualdade).

É necessária essa verificação, pois, ao elevarmos os dois membros de uma equação a uma potência, podem aparecer na equação obtida raízes estranhas à equação dada. Observe alguns exemplos de resolução de equações irracionais no conjunto dos reais.

• 
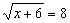
  Solução:
  
  Logo, V= {58}.

• 
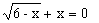
  Solução:
  
  Logo, V= { -3}; note que 2 é uma raiz estranha a essa equação irracional.

• 
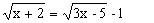
  Solução:
  
  
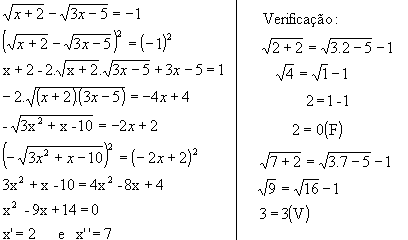
  Logo, V= { 7 }; note que 2 é uma raiz estranha a essa equação irracional.

• 
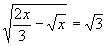
  Solução:
  
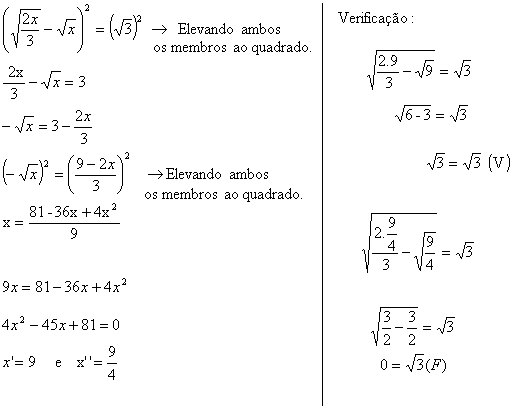
  Logo, V={9}; note que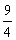 é uma raiz estranha a essa equação irracional.