Você está em Ensino fundamental > Equações do 2º grau ▼
📄 O que é uma equação do 2º grau?
📄 Raízes de uma equação do 2º grau
📄 Resolução de equações incompletas
📄 Resolução de equações completas
📄 Discriminante
📄 Equações literais
📄 Relações entre os coeficientes e as raízes
📄 Composição de uma equação de 2º grau
📄 Forma fatorada
📄 Equações biquadradas
📄 Resolução de uma equação biquadrada
📄 Composição da equação biquadrada
📄 Equações irracionais
📄 Sistemas de equações do 2º grau
📄 Problemas do 2º grau
📄 Outros exemplos
📄 Raízes de uma equação do 2º grau
📄 Resolução de equações incompletas
📄 Resolução de equações completas
📄 Discriminante
📄 Equações literais
📄 Relações entre os coeficientes e as raízes
📄 Composição de uma equação de 2º grau
📄 Forma fatorada
📄 Equações biquadradas
📄 Resolução de uma equação biquadrada
📄 Composição da equação biquadrada
📄 Equações irracionais
📄 Sistemas de equações do 2º grau
📄 Problemas do 2º grau
📄 Outros exemplos
Problemas do 2º grau
Para resolução de problemas do 2º grau, devemos seguir etapas:
Sequência prática:
- Estabeleça a equação ou sistema de equações que traduzem o problema para a linguagem matemática.
- Resolva a equação ou o sistema de equações.
- Interprete as raízes encontradas, verificando se são compatíveis com os dados do problema.
Observe agora, a resolução de alguns problemas do 2º grau:
- Determine dois números inteiros
consecutivos tais que a soma de seus inversos seja
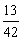 .
.
Solução:
Representamos um número por x, e por x + 1 o seu consecutivo. Os seus inversos serão representados por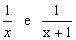 .
.
Temos então a equação: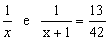 .
.
Resolvendo-a:
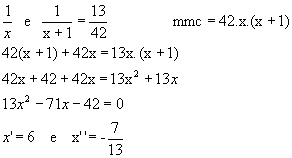
Observe que a raiz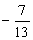 não é utilizada, pois não se trata de número inteiro.
não é utilizada, pois não se trata de número inteiro.
Resposta: Os números pedidos são, portanto, 6 e o seu consecutivo 7.
- Um número de dois algarismos é tal
que, trocando-se a ordem dos seus algarismos, obtém-se um número que o
excede de 27 unidades. Determine esse número, sabendo-se que o produto dos
valores absolutos dos algarismos é 18.
Solução:
Representamos um número por 10x + y, e o número com a ordem dos algarismos trocada por 10y + x.
Observe:
Número: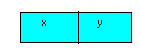
 10x + y
10x + y
Número com a ordem dos algarismos trocada: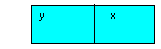
 10y + x.
10y + x.
Temos, então, o sistema de equações:
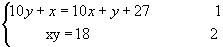
Resolvendo o sistema, temos:
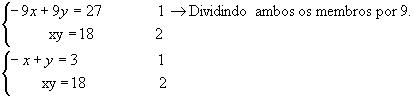
Isolando y na primeira equação:
-x + y = 3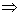 y= x
+ 3
y= x
+ 3
Substituindo y na segunda equação:
xy = 18
x ( x + 3) = 18
x2 + 3x = 18
x2 + 3x - 18 = 0
x'= 3 e x''= -6
Determinando y para cada um dos valores de x, obtemos:
y'= 3 + 3 = 6
y''= -6 + 3 = -3
Logo, o conjunto verdade do sistema é dado por: V= { (3,6), ( -6, -3)}.
Desprezando o par ordenado de coordenadas negativas, temos para solução do problema o número 36 ( x=3 e y=6).
Resposta: O número procurado é 36.
Próximo: Outros exemplos
Como referenciar: "Equações do 2º grau" em Só Matemática. Virtuous Tecnologia da Informação, 1998-2026. Consultado em 29/01/2026 às 14:27. Disponível na Internet em https://www.somatematica.com.br/fundam/equacoes2/equacoes2_16.php




























