Resolução de uma equação biquadrada

Na resolução de uma equação biquadrada em IR, devemos substituir sua variável, transformando-a numa equação do 2º grau. Observe agora o procedimento que deve ser utilizado.

Sequência prática:

• Substitua x⁴ por y² (ou qualquer outra incógnita elevada ao quadrado) e x² por y.

• Resolva a equação ay² + by + c = 0.

• Determine a raiz quadrada de cada uma da raízes ( y'e y'') da equação ay² + by + c = 0.
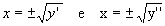
  Essas duas relações indicam-nos que cada raiz positiva da equação ay² + by + c = 0 dá origem a duas raízes simétricas para a biquadrada: a raiz negativa não dá origem a nenhuma raiz real para a mesma.

Exemplos:

• Determine as raízes da equação biquadrada x⁴ - 13 x² + 36 = 0.
  Solução:
  Substituindo x⁴ por y² e x² por y, temos:
  y² - 13y + 36 = 0
  
  Resolvendo essa equação, obtemos:
  y'=4     e      y''=9
  
  Como x²= y, temos:
  
  
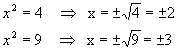
  Logo, temos para conjunto verdade: V={ -3, -2, 2, 3}.

• Determine as raízes da equação biquadrada x⁴ + 4x² - 60 = 0.
  Solução:
  Substituindo x⁴ por y² e x² por y, temos:
  y² + 4y - 60 = 0
  
  Resolvendo essa equação, obtemos:
  y'=6   e  y''= -10
  
  Como x²= y, temos:
  

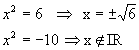
  Logo, temos para o conjunto verdade:.

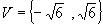• Determine a soma das raízes da equação .
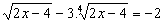  Solução:
  Utilizamos o seguinte artifício:
  
  
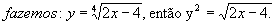
  Assim:
  y² - 3y = -2
  y² - 3y + 2 = 0
  y'=1  e  y''=2
  
  Substituindo y, determinamos:
  
  
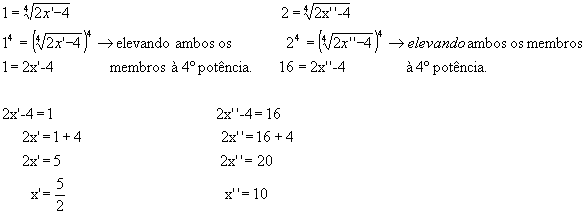
  Logo, a soma das raízes é dada por:
  

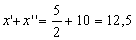
Resolução de equações da forma: ax²ⁿ  +  bxⁿ  + c = 0

Esse tipo de equação pode ser resolvida da mesma forma que a biquadrada. Para isso, substituimos xⁿ por y, obtendo:

ay² + by + c = 0, que é uma equação do 2º grau.

Exemplo:

• Resolva a equação x⁶ + 117x³ - 1.000 = 0.
  Solução:
  Fazendo x³=y, temos:
  y² + 117y - 1.000 = 0
  

  Resolvendo a equação, obtemos:
  y'= 8  e  y''= - 125
  Então:
  
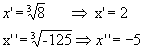
  Logo, V= {-5, 2 }.