Teste T para duas amostras não relacionadas

O teste t é muito utilizado em pesquisa para verificar se a diferença observada entre duas médias  obtidas nas amostras é considerada grande para ser significativa.

Supondo que dois estabelecimentos discutem qual possui clientes mais satisfeitos. Para mensurar o grau de satisfação junto aos clientes, resolve-se realizar uma pesquisa de satisfação aplicando um questionário com questões intervalares de 5 pontos.

O cliente A obteve média geral 2,85 e o cliente B obteve média geral 3,45. Supostamente, conclui-se que o cliente B possui clientes mais satisfeitos que A.

O teste t visa justamente comprovar se tal diferença é significativa e explicar se as diferenças entre as médias ocorrem devido ao erro amostral ou não.

Quando trabalha-se com amostras pequenas, existe uma tendência para que as médias das amostras seja realmente diferentes, mesmo que originem-se da mesma população. Neste caso o teste t, objetiva justamente verificar se o grau de diferença entre os dois conjuntos  pode ser devido  a fatores outros que não o erro de amostragem.

Condições para aplicação

- Somente para questões intervalares;

- Quando a variância da população for desconhecida;

- n pode ser de qualquer tamanho.

Procedimento de execução

1. Determinar H₀, não havendo diferenças entre as médias;

2. Determinar H₁, para a existência de diferença entre as médias;

3. Estabelecer um nível de significância;

4. Calcular t, onde os graus de liberdade, φ  = n₁ + n₂ – 2

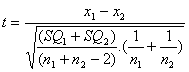
onde SQ é a soma dos quadrados e x1 e x2 são as médias de cada grupo.

A fórmula acima pode divergir em alguns livros de estatísticas que abordem amostras desiguais, no entanto, a mesma contempla amostras de tamanhos iguais ou não.

Comparar o t tabelado com t calculado e rejeitar a hipótese nula em prol da alternativa, em caso de encontrar-se t calculado maior que o tabelado.

Exemplo

Sendo t tabelado igual a 2,02 com 38 graus de liberdade e t calculado igual a 1,77, rejeita-se a hipótese nula em prol da hipótese verdadeira.

Conclui-se, portanto que os dois grupos de clientes estão satisfeitos e que provavelmente as diferenças entre as médias sejam devido ao erro de amostragem.