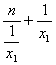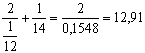Medidas de tendência central

Há várias medidas de tendência central, entretanto neste material será realizado o estudo apenas daquelas que forem as mais significativas para a teoria de pesquisa mercadológica.

As mais importante medidas de tendência central, são a média aritmética, média aritmética para dados agrupados, média aritmética ponderada, mediana, moda, média geométrica, média harmônica, quartis.

Quando se estuda variabilidade, as medidas mais importantes são: amplitude, desvio padrão e variância.

Medidas	Fórmula	Exemplo
Média aritmética
Média aritmética para dados agrupados
Média aritmética ponderada		4 (4) + 6 (9) = 7
Mediana	1) Se n é impar, o valor é central, 2) se n é par, o valor é a média dos dois valores centrais.	12 13 14 = 13 12 13 14 15 = 13,5
Moda	Valor que ocorre com mais frequência.	22 23 22 22 34 45 = 22
Média geométrica	G = ⁿv X₁X₂...	³v12 x 14 x 16 = 13,90
Média harmônica
Quartis

Exemplo de calculo de quartil:

Para a amostra abaixo, calcular o primeiro e o terceiro quartis:

1) Valores em ordem crescente e cálculo de p(i).

13,3 13,5 17,2 13,8 12,3 12,7 13,0 14,5 14,9 15,8 13,1 13,3 14,1

12,3 12,7 13,0 13,1 13,3 13,3 13,5 13,8 14,1 14,5 14,9 15,8 17,2

X (i)

12,3

12,7

13,0

13,1

13,3

13,5

13,8

14,1

14,5

14,9

15,8

17,2

0,038

0,115

0,192

0,269

0,346

0,423

0,500

0,577

0,654

0,731

0,808

0,885

0,962

2) Valores imediatamente acima e abaixo de 0,25 (13,0 e 13,1), associados com p_(inf) = 0,192 e p _(sup) = 0,269

Valores imediatamente acima e abaixo de 0,75: x_(inf) = 14,5 e x _(sup) = 14,9, associados com p_(inf) = 0,731 e p_(sup) = 0,808:

O valor para o segundo quartil é representado pela mediana (13,5).

Próximo: Variabilidade

Como referenciar: "Medidas de tendência central (Estatística básica para pesquisa de mercado)" em Só Matemática. Virtuous Tecnologia da Informação, 1998-2024. Consultado em 05/12/2024 às 21:55. Disponível na Internet em https://www.somatematica.com.br/estat/ap19.php

Medidas de tendência central

Curso on-line do Só Matemática