Dispositivo prático de Briot-Ruffini

Para efetuarmos a divisão de um polinômio P(x) por um binômio da forma (x –), podemos utilizar o dispositivo prático de Briot-Ruffini.

Vamos efetuar a divisão de  por x - 2 através desse dispositivo. Acompanhe o roteiro para a resolução:

1º) Colocamos a raiz do divisor e os coeficientes do dividendo (ordenadamente do termo de maior grau para o termo de menor grau, completando com zero os termos que não aparecem) no dispositivo:

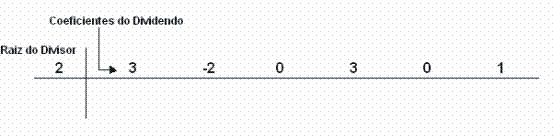
2º) Abaixamos o primeiro coeficiente do dividendo:

3º) Multiplicamos a raiz do divisor pelo coeficiente repetido e somamos o produto com o segundo coeficiente do dividendo, colocando o resultado abaixo deste:

4º) Multiplicamos a raiz do divisor pelo número colocado abaixo do 2º coeficiente e somamos o produto com o 3º coeficiente, colocando o resultado abaixo deste, e assim sucessivamente:

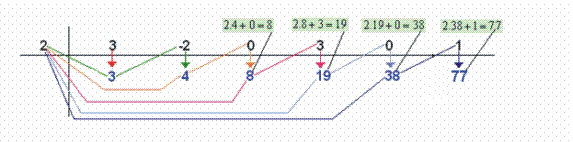
5º) Fazemos um traço entre o último e o penúltimo números obtidos. O último número é igual ao resto da divisão e os números que ficam à esquerda deste são os coeficientes do quociente:

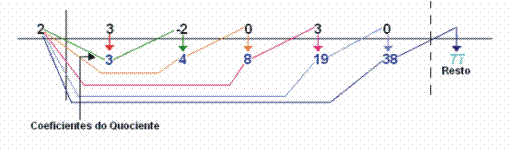
Portanto, . 

Exemplo

Obtenha o quociente e o resto da divisão de x³ - 3x² + 5x - 1 por 2x - 1:

Resolução

Temos:
Para aplicarmos o dispositivo de Briot-Ruffini, o coeficiente de x no divisor deve ser 1. Nesse caso, utilizamos o seguinte artifício:

Fazemos :

Aplicando o dispositivo de Briot-Ruffini:

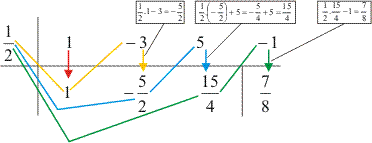
Como :

Portanto,  e .