📄 Raiz de um polinômio
📄 Polinômios idênticos
📄 Operações com polinômios
📄 Divisão de polinômios
📄 Teorema do resto e Teorema de D'Alembert
📄 Divisão de um polinômio por (x-a)(x-b)
📄 Dispositivo de Briot-Ruffini
📄 Divisões sucessivas
📄 Equações polinomiais
📄 Multiplicidade de uma raiz
📄 Raízes nulas, complexas e racionais
📄 Relações de Girard
Teorema do resto
Vamos calcular o resto da divisão de 
:
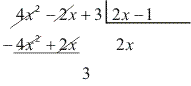R(x) = 3
A raiz do divisor é 
.
Note que: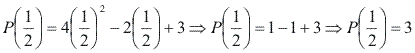 
Ou seja, quando B(x) é um polinômio de grau 1, o resto é igual ao valor numérico de P(x) quando x assume o valor da raiz de B(x).
Para demonstrar esse fato, vamos efetuar:
Note que o grau do resto é 0, pois é menor que o grau do divisor, que é 1. Assim, o resto é uma constante r.
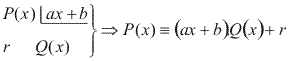
Efetuando 
, temos:
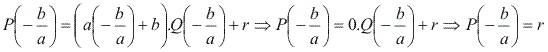
Assim, podemos enunciar o seguinte teorema:
Teorema do resto O resto da divisão de um polinômio P(x) pelo binômio ax + b é igual ao valor numérico desse polinômio para |
, ou seja, 
.Exemplo
Calcule o resto da divisão de P(x) = x² + 5x - 1 por B(x) = x + 1:
Resolução
Achamos a raiz do divisor:
x + 1= 0 
x = - 1
Pelo teorema do resto, sabemos que o resto é igual a P(-1):
P(-1) = (-1)² + 5.(-1) -1 
P(- 1) = - 5 = r
Portanto, o resto da divisão de x² + 5x - 1 por x + 1 é - 5.
Note que P(x) é divisível por ax + b quando r = 0, ou seja, quando 
. Daí vem o enunciado do seguinte teorema:
Teorema de D’Alembert Um polinômio P(x) é divisível pelo binômio 1 se e somente se |
. O caso mais importante da divisão de um polinômio P(x) é aquele em que o divisor é da forma (x - 
).
Note que 
é a raiz do divisor. Então o resto da divisão de P(x) por (x –
) é:
r = P(
)
Assim:
P(x) é divisível por (x – |
) quando r = 0, ou seja, quando P(
) = 0.Exemplo
Determine o valor de p, para que o polinômio 
seja divisível por x – 2:
Resolução
Para que P(x) seja divisível por x – 2 devemos ter P(2) = 0, pois 2 é a raiz do divisor:
Assim, para que 
seja divisível por x – 2 devemos ter p = 19.
