📄 Raiz de um polinômio
📄 Polinômios idênticos
📄 Operações com polinômios
📄 Divisão de polinômios
📄 Teorema do resto e Teorema de D'Alembert
📄 Divisão de um polinômio por (x-a)(x-b)
📄 Dispositivo de Briot-Ruffini
📄 Divisões sucessivas
📄 Equações polinomiais
📄 Multiplicidade de uma raiz
📄 Raízes nulas, complexas e racionais
📄 Relações de Girard
Divisão de polinômios
Vamos pensar em uma divisão de números naturais. Dividir 7 por 5 significa obter o quociente 1 e o resto 2. Podemos escrever:
![]()
Agora vamos pensar na divisão do polinômio A(x) pelo polinômio não-nulo B(x), que gera o quociente Q(x) e o resto R(x).
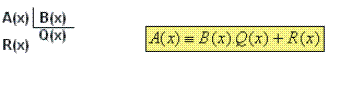
Nessa divisão:
- A(x) é o dividendo;
- B(x) é o divisor;
- Q(x) é o quociente;
- R(x) é o resto da divisão.
O grau de R(x) deve ser menor que o grau de B(x) ou R(x) = 0.
Quando A(x) é divisível por B(x), dizemos que a divisão é exata, isto é, R(x) = 0.
Exemplo 1
Determine o quociente de ![]() :
:
Resolução
- Dividimos o termo de maior grau do dividendo pelo termo de maior grau do divisor. O resultado será um termo do quociente:
![]()
- Multiplicamos x² por B(x) e subtraímos o produto de A(x), obtendo o primeiro resto parcial:
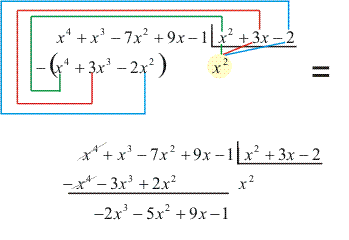
- Dividimos o termo de maior grau do primeiro resto parcial pelo termo de maior grau do divisor, e obteremos como o resultado um termo do quociente:
![]()
- Multiplicamos -2x por B(x) e subtraímos o produto do primeiro resto parcial, obtendo o segundo resto parcial:
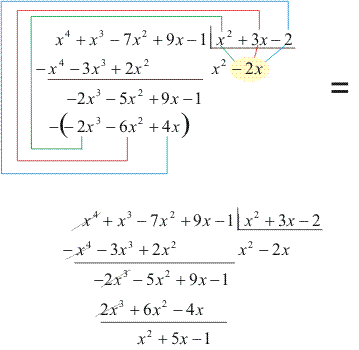
- Dividimos o termo de maior grau do segundo resto parcial pelo termo de maior grau do divisor, e obteremos como o resultado um termo do quociente:
![]()
- Multiplicamos 1 por B(x) e subtraímos o produto do segundo resto parcial:
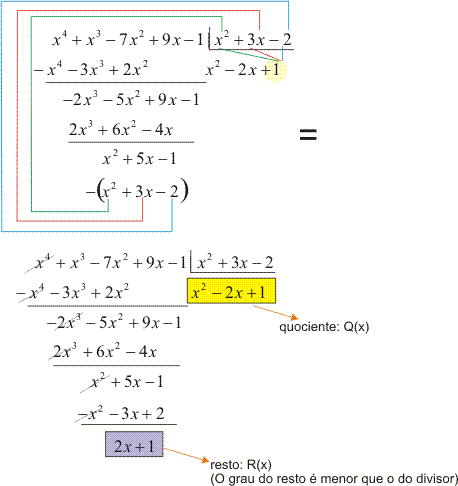
Como o grau do resto é menor que o grau do divisor, a divisão está encerrada.
Verificamos que:
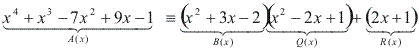
Exemplo 2
Determine o quociente de ![]() :
:
Resolução
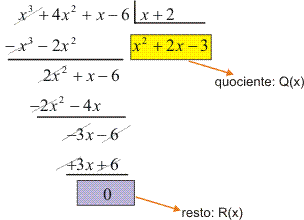
Verificamos facilmente que:
![]()
Nesses dois exemplos, utilizamos o método da chave para efetuar a divisão de polinômios.
Pelos exemplos verificamos que:
grau do quociente = grau do dividendo – grau do divisor




























