Função crescente e função decrescente

Dada uma função f: AB, dizemos que f é crescente em algum conjunto A’A, se, e somente se, para quaisquer x₁ A’ e x₂ A’, com x₁<x₂, tivermos f(x₁)<f(x₂).

Por exemplo, a função f: IRIR definida por f(x)=x+1 é crescente em IR, pois:
x₁<x₂ => x₁+1<x₂+1 => f(x₁)<f(x₂)

Ou seja: quando os valores do domínio crescem, suas imagens também crescem.

Por outro lado, dada uma função f: AB, dizemos que f é decrescente em algum conjunto A’ A, se, e somente se, para quaisquer x₁ A’ e x₂ A’, com x₁<x₂, tivermos f(x₁)>f(x₂).

Por exemplo, a função f: IRIR definida por f(x)=-x+1 é decrescente em IR, pois:
x₁<x₂ => -x₁>-x₂ => -x₁+1>-x₂+1 => f(x₁)>f(x₂).

Ou seja: quando os valores do domínio crescem, suas correspondentes imagens decrescem. Exemplos:

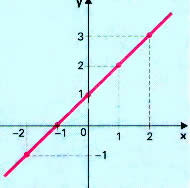
Este é um exemplo de função crescente. Podemos notar no gráfico que à medida que os valores de x vão aumentando, suas imagens também vão aumentando.

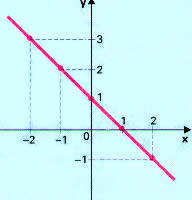
Este é um exemplo de função decrescente. Podemos notar no gráfico que à medida que os valores de x vão aumentando, suas imagens vão diminuindo.