Construção do gráfico cartesiano de uma função

Para construir o gráfico de uma função f, basta atribuir valores do domínio à variável x e, usando a sentença matemática que define a função, calcular os correspondentes valores da variável y.

Vamos construir o gráfico da função definida por y=x/2. Escolhemos alguns valores para o domínio, como por exemplo D={2,4,6,8}. Agora calculamos os respectivos valores de y. Assim temos:

x=2 y=2/2 = 1
x=4 y=4/2 = 2
x=6 y=6/2 = 3
x=8 y=8/2 = 4

Então, montamos a seguinte tabela:

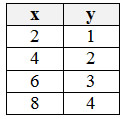
Identificamos os pontos encontrados no plano cartesiano:

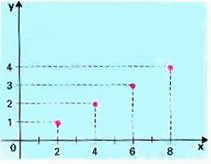
O gráfico da função será uma reta que passará pelos quatro pontos encontrados. Basta traçar a reta, e o gráfico estará construído.

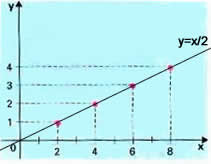
Obs: para desenhar o gráfico de uma reta são necessários apenas dois pontos. No exemplo acima escolhemos 4 pontos, mas bastaria escolher dois elementos do domínio, encontrar suas imagens, e logo após traçar a reta que passa por esses 2 pontos.