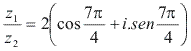📄 Igualdade de números complexos
📄 Conjugado de um número complexo
📄 Adição e subtração na forma algébrica
📄 Multiplicação e divisão na forma algébrica
📄 Potências de i
📄 Módulo e argumento
📄 Forma trigonométrica ou polar
📄 Multiplicação e divisão na forma trigonométrica
📄 Potenciação e radiciação na forma trigonométrica
Multiplicação e divisão de números complexos na forma trigonométrica
Algumas operações com números complexos são mais facilmente efetuadas quando os números estão na forma trigonométrica.
Acompanhe a seguir como funcionam as operações de multiplicação de divisão.
Multiplicação
Considere dois números complexos na forma trigonométrica 
. O produto 
é dado por:
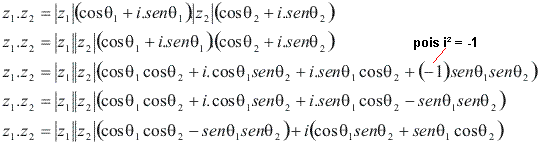
Lembrando das fórmulas de adição de arcos:
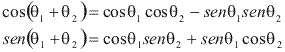
Assim:
 |
Observe que o produto 
é um número complexo cujo módulo é o produto dos módulos dos fatores e cujo argumento é a soma dos argumentos dos fatores.
Exemplo
Calcule o produto 
, com 
:
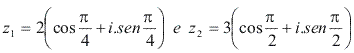Resolução
- O módulo de
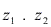é produto 
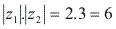. - O argumento de
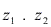é dado pela soma 
.
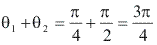Assim:
Divisão
Considere dois números complexos na forma trigonométrica:
.
O quociente 
é dado por:
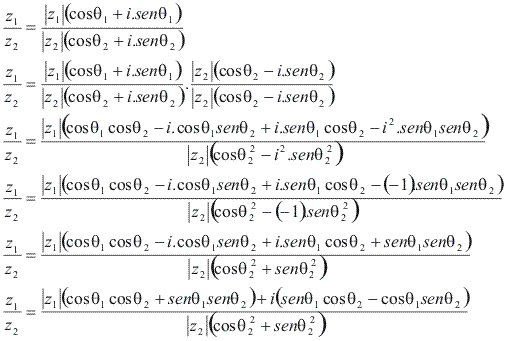
Lembrando das fórmulas de diferença de arcos:
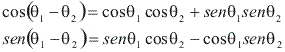
E da relação trigonométrica fundamental: 
Assim:
 |
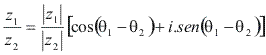Observe que o quociente 
é um número complexo cujo módulo é o quociente dos módulos do dividendo e do divisor, e cujo argumento é a diferença dos argumentos do dividendo e do divisor.
Exemplo
Calcule o quociente 
, com 
:
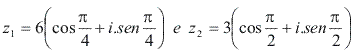Resolução
- O módulo de
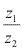é o quociente 
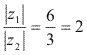. - O argumento de
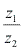é dado pela diferença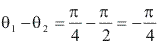 
Como 
fazemos: 
Assim:
