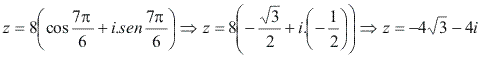Forma trigonométrica ou polar

Considere o número complexo z = a + bi, de módulo e argumento .

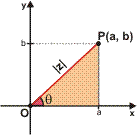
Temos que:

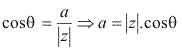
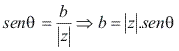
Substituindo em z = a + bi, temos:

Essa expressão é denominada forma trigonométrica ou polar do complexo z.

Exemplo 1

Escreva na forma trigonométrica o número complexo z = 1 + i:

Resolução

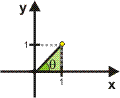
Módulo:

Argumento:

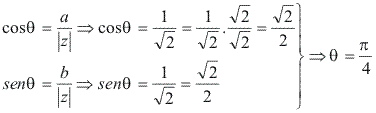
Portanto, z pode ser escrito na forma trigonométrica:

Exemplo 2

Escreva na forma trigonométrica o número complexo z = 8i:

Resolução

Módulo:

Argumento:

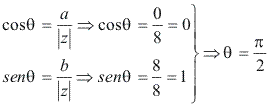
Portanto, z pode ser escrito na forma trigonométrica:

Exemplo 3

Escreva na forma algébrica o número complexo :
Resolução

Essa transformação é imediata, pois basta substituir  e  pelos respectivos valores: