Baricentro de um triângulo

Observe o triângulo da figura a seguir, em que M, N e P são os pontos médios dos lados , respectivamente. Portanto, são as medianas desse triângulo:

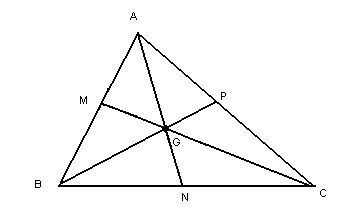
Chamamos de baricentro (G) o ponto de intersecção das medianas de um triângulo. Esse ponto divide a mediana relativa a um lado em duas partes: a que vai do vértice até o baricentro tem o dobro da mediana da que vai do baricentro até o ponto médio do lado. Veja:

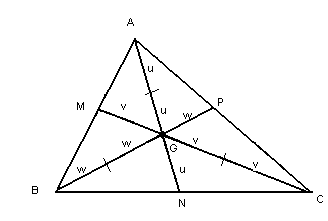
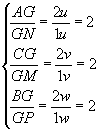
Cálculo das coordenadas do baricentro

Sendo A(X_A, Y_A), B(X_B, Y_B) e C(X_C, Y_C) vértices de um triângulo, se N é ponto médio de , temos:

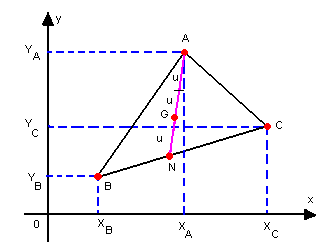
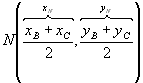
Mas:

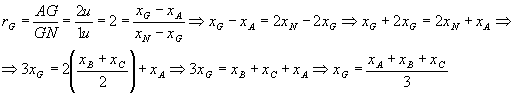
Analogamente, determinamos . Assim: