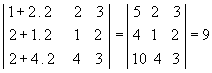📄 Menor complementar
📄 Cofator
📄 Teorema de Laplace
📄 Regra de Sarrus
📄 Propriedades dos determinantes
📄 Propriedades (parte 2)
📄 Propriedades (parte 3)
Propriedades dos determinantes
Os determinantes associados a matrizes quadradas de ordem n apresentam as seguintes propriedades:
P1) Quando todos os elementos de uma fila (linha ou coluna) são nulos, o determinante dessa matriz é nulo. Exemplo:
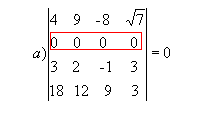
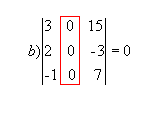
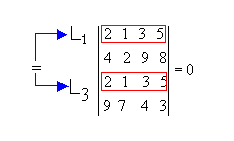
P2) Se duas filas de uma matriz são iguais, então seu determinante é nulo. Exemplo:
P3) Se duas filas paralelas de uma matriz são proporcionais, então seu determinante é nulo. Exemplo:
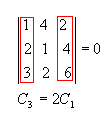
P4) Se os elementos de uma fila de uma matriz são combinações lineares dos elementos correspondentes de filas paralelas, então seu determinante é nulo. Exemplos:
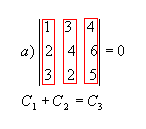
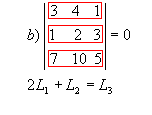
P5) Teorema de Jacobi: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas. Exemplo:
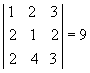
Substituindo a 1ª coluna pela soma dessa mesma coluna com o dobro da 2ª, temos: