Convergência absoluta

Uma série é absolutamente convergente se a série dos módulos

é convergente.

Por exemplo, a série alternada
é absolutamente convergente, pois a série dos módulos é uma série-p, com p=2 > 1 e, portanto, convergente.

Teorema

Se uma série infinita é absolutamente convergente, então a série é convergente.

Teste de D'Alembert

Seja uma série de termos não nulos e seja 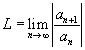 . Então:

* Se L < 1, a série é absolutamente convergente.

* Se L > 1, (incluindo L = 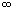), a série é divergente.

* Se L = 1, o teste falha (nada se pode afirmar).