Teste de Leibniz

Uma série alternada CONVERGE se:

* Seu termo genérico, em módulo, tende a zero.

* A série dos módulos é decrescente.

Há três maneiras diferentes de verificar se a série dos módulos é decrescente.

a) verificar se, para todo "k" inteiro positivo, .

b) verificar se, para todo "k" inteiro positivo, .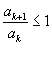

c) considerar a função f(x) = f(n) e verificar o sinal de sua derivada. Se f'(x)<0, então f é decrescente.