Série geométrica

Uma série geométrica é do seguinte tipo:

sendo a0 e r a razão.

Ex: 1 + 2 + 4 + 8 + 16 + ...

a = 1
r =

Soma de uma série geométrica

A série geométrica 

Converge e tem soma    se | r | < 1.
Diverge se | r | 1.

Teste da comparação

Sejam  e   duas séries de termos positivos. Então:

* Se      , sendo "c" um número real, então as séries são ambas convergentes ou ambas divergentes.

* Se   e se converge, então também converge.

* Se     e se  diverge, então também diverge.

OBS: Se a_n é expressa por uma fração, devemos considerar tanto no numerador, quanto no denominador de b_n somente os termos de maior importância.

Ex: Verifique se a série dada converge ou diverge:

    é uma série geométrica de razão 1/3, logo ela é convergente. Aplicando o teste da comparação, temos:

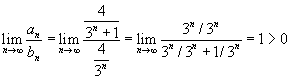
Logo, conclui-se que a série converge.