Fórmula do termo geral de uma PA

Já sabemos que numa PA:

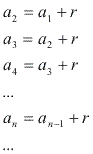
Note que podemos escrever todos os termos de uma PA em função de e r:

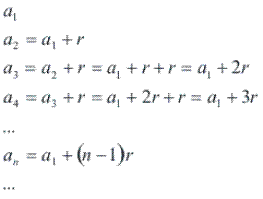
Portanto, o termo geral da PA será dado pela fórmula:

, n

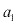• = primeiro termo
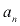• = enésimo termo
• r = razão
• n = número de termos

Exemplo 1

Determine o termo geral da PA (-19, -15, -11, ...):

Resolução

O termo geral da PA (-19, -15, -11, ...) é .

Exemplo 2

Determine o 16º termo da PA (3, 9, 15, ...):

Resolução

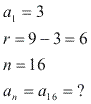
Portanto, o 16º termo da PA (3, 9, 15, ...) é 93.

Exemplo 3

Interpole seis meios aritméticos entre -8 e 13:

Resolução

Do enunciado temos que:

Encontrada a razão, basta interpolar os meios aritméticos: (-8, -5, -2, 1, 4, 7, 10, 13).

Exemplo 4

Quantos múltiplos de 5 há entre 101 e 999?

Resolução

• O primeiro múltiplo de 5 depois de 101 é 105, portanto 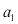= 105;
• O último múltiplo de 5 antes de 999 é 995, portanto 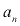= 995;
• A razão é 5, pois estamos nos referindo a múltiplos de 5.

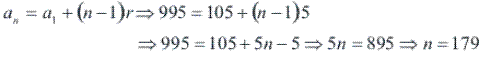
Assim, concluímos que existem 179 múltiplos de 5 entre 101 e 999.

Exemplo 5

Sabendo que numa PA o 2º termo é 9 e o 11º termo é 45, escreva essa PA:

Resolução
Vamos escrever esses termos em função de e r:

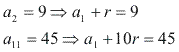
Montamos um sistema de equações:

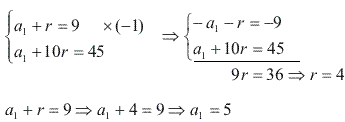
Portanto, a PA é (5, 9, 13, 17, ...).