|
Funções
Logarítmica e Exponencial
- DOMÍNIO
E IMAGEM DAS FUNÇÕES INVERSAS
A equação seguinte
implica em certas relações entre os domínios e as imagens de f e  .
Por exemplo, na primeira equação a quantidade f (x) é uma
entrada de,
assim pontos nas imagens de f estão no domínio de;
e na segunda equação, a quantidade(x)é
uma entrada de f, sendo que pontos na imagem de
estão no domínio de f. Tudo isso sugere as seguintes relações:
domínio de
= imagem de f
imagem de
= domínio de f |
Uma vez que f e g satisfazem duas condições:
- g(f(x)) = x para todo x no domínio de f
- f(g(y)) = y para todo y no domínio de g
concluímos que elas são inversas. Assim temos o seguinte resultado.
|
Se uma equação y = f (x) pode ser resolvida para
x
como uma função de y, então f tem uma inversa e a equação resultante é
x
= (y) |
- UM MÉTODO PARA ACHAR INVERSAS
Exemplo
Ache a inversa de f (x) = 
Solução.
Podemos achar uma fórmula para (y)
resolvendo a equação
y =
para x como uma função de y. Os
cálculos são:
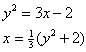
da qual tem-se que
Até aqui, fomos bem-sucedidos em obter uma fórmula para ;
contudo não estamos realmente completos, uma vez que não há nenhuma garantia
de que o domínio natural associado é o domínio completo para .
Para determinar se isto é o que acontece, examinaremos a imagem de y = f (x)
= .
A imagem consiste de todos os y no intervalo  ,
assim este intervalo é também o domínio de (y);
logo a inversa de f é dada pela fórmula
OBSERVAÇÃO. Quando
uma fórmula para
for obtida resolvendo-se a equação y = f(x) para x como
uma função de y, a fórmula resultante tem y como a variável
independente. Se for preferível ter x como a variável independente para
,
então há duas formas: você pode resolver y = f(x) para x
com uma função de y, e então substituir y por x na
fórmula final para
, ou então você pode trocar x e y na equação original
e resolver a equação x = f(y) para y em termos de x.
Neste caso a equação final será y = (x).
<<
Voltar para Ensino Superior
|
