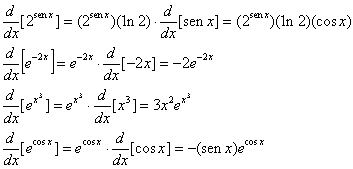Derivadas das funções exponenciais

Para obter uma fórmula para a derivada de funções exponenciais

y =

reescrevemos esta equação como

x =

e diferenciamos implicitamente usando   para obter

que podemos reescrever usando y =   como

Assim, mostrando que se   for uma função diferenciável, então sua derivada em relação a x é

No caso especial onde b = e temos 1n e = 1n, assim      torna-se

Além disso, se u for uma função diferenciável de x, então tem-se a partir de      e       que

OBSERVAÇÃO.É importante distinguir entre diferenciar (expoente variável e base constante) e (base variável e expoente constante).

Exemplo

Os cálculos a seguir usam