Multiplicação de matrizes

O produto de uma matriz por outra não é determinado por meio do produto dos seus respectivos elementos.

Assim, o produto das matrizes A = (a_ij)_{m x p}  e B = (b_ij)_{p x n} é a matriz C = (c_ij) _{m x n}, em que cada elemento c_ij é obtido por meio da soma dos produtos dos elementos correspondentes da i-ésima linha de A pelos elementos da j-ésima coluna B.

Vamos multiplicar as matrizes para entender como se obtém cada elemento c_ij:

• 1ª linha e 1ª coluna

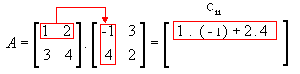
• 1ª linha e 2ª coluna

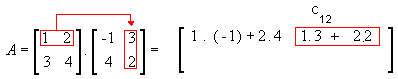
• 2ª linha e 1ª coluna

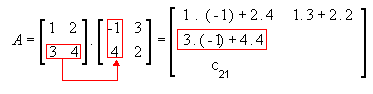
• 2ª linha e 2ª coluna

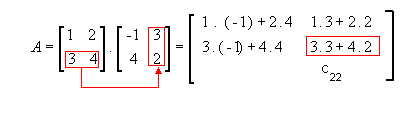
Assim, .

Agora observe o que aconteceria se fosse feito o contrário, ou seja, multiplicar B por A:

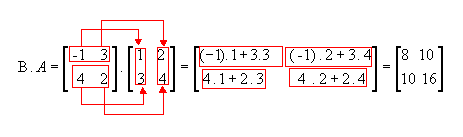
Portanto, .A, ou seja, para a multiplicação de matrizes não vale a propriedade comutativa.

Vejamos outro exemplo com as matrizes :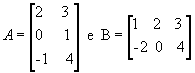

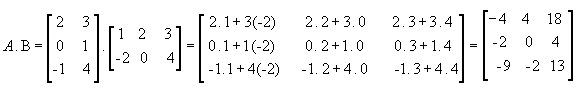
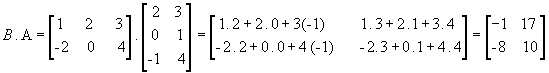
Da definição, temos que a matriz produto A . B só existe se o número de colunas de A for igual ao número de linhas de B:

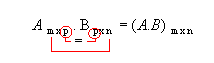
A matriz produto terá o número de linhas de A (m) e o número de colunas de B (n):

• Se A_{3 x 2} e B _{2 x 5} , então ( A . B ) _{3 x 5}

• Se A _{4 x 1} e B _{2 x 3}, então não existe o produto

• Se A _{4 x 2} e B _{2 x 1}, então ( A . B ) _{4 x 1}
     

Propriedades

Verificadas as condições de existência para a multiplicação de matrizes, valem as seguintes propriedades:

a) associativa: (A . B) . C = A . (B . C)

b) distributiva em relação à adição: A . (B + C) = A . B + A . C ou (A + B) . C = A . C + B . C

c) elemento neutro: A . I_n = I_n . A = A, sendo I_n a matriz identidade de ordem n

Vimos que a propriedade comutativa, geralmente, não vale para a multiplicação de matrizes. Não vale também o anulamento do produto, ou seja: sendo 0 _{m x n} uma matriz nula, A .B =0_{m x n} não implica, necessariamente, que A = 0_{m x n} ou B = 0_{m x n}.

Matriz inversa

Dada uma matriz A, quadrada, de ordem n, se existir uma matriz A', de mesma ordem, tal que A . A' = A' . A = I_n , então A' é matriz inversa de A . Representamos a matriz inversa por A^-1 .