Equações impossíveis e identidades

• Sendo 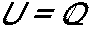, considere a seguinte equação: 2.(6x - 4) = 3.(4x - 1).

Observe agora a sua resolução:

2 . 6x - 2 . 4 = 3 . 4x - 3 . 1

12x - 8 = 12x - 3 

12x - 12x = - 3 + 8

0 . x = 5

Como nenhum número multiplicado por zero é igual a 5, dizemos que a equação é  impossível e, portanto, não tem solução. Logo, V =  Ø.

Assim, uma equação do tipo ax + b = 0 é impossível quando e

•  Sendo 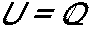, considere a seguinte equação: 10 - 3x - 8 = 2 - 3x.

Observe a sua resolução:

-3x + 3x = 2 - 10 + 8

0 . x = 0 

Como todo número multiplicado por zero é igual a zero, dizemos que a equação possui infinitas soluções. Equações desse tipo, em que qualquer valor atribuído à variável torna a equação verdadeira, são denominadas identidades.