Probabilidade

Introdução

A história da teoria das probabilidades teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade. A teoria da probabilidade permite que se calcule a chance de ocorrência de um número em um experimento aleatório.

Experimento aleatório

É aquele experimento que, quando repetido em iguais condições, pode fornecer resultados diferentes, ou seja, são resultados explicados ao acaso. Quando se fala de tempo e possibilidades de ganho na loteria, a abordagem envolve cálculo de experimento aleatório.

Espaço amostral

É o conjunto de todos os resultados possíveis de um experimento aleatório. A letra que representa o espaço amostral é S.

Exemplo:

Lançando uma moeda e um dado, simultaneamente, sendo S o espaço amostral, constituído pelos 12 elementos:

S = {K1, K2, K3, K4, K5, K6, R1, R2, R3, R4, R5, R6}

1. Escreva explicitamente os seguintes eventos:
   A={caras e um número par aparece}
   B={um número primo aparece}
   C={coroas e um número ímpar aparecem}
    
2. Idem, o evento em que:
   a) A ou B ocorrem;
   b) B e C ocorrem;
   c) Somente B ocorre.

1. Quais dos eventos A, B e C são mutuamente exclusivos?

Resolução:

1. Para obter A, escolhemos os elementos de S constituídos de um K e um número par:  A={K2, K4, K6};
   Para obter B, escolhemos os pontos de S constituídos de números primos: B={K2,K3,K5,R2,R3,R5};
   Para obter C, escolhemos os pontos de S constituídos de um R e um número ímpar: C={R1,R3,R5}.

1. (a) A ou B = AUB = {K2,K4,K6,K3,K5,R2,R3,R5}
   (b) B e C = BC = {R3,R5}
   (c) Escolhemos os elementos de B que não estão em A ou C:
   B   A^c    C^c   =   {K3,K5,R2}

1. A e C são mutuamente exclusivos, porque A C =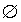
    

Conceito de probabilidade

Se em um fenômeno aleatório as possibilidades são igualmente prováveis, então a probabilidade de ocorrer um evento A é:

Por, exemplo, no lançamento de um dado, um número par pode ocorrer de 3 maneiras diferentes dentre 6 igualmente prováveis, portanto, P = 3/6= 1/2 = 50%.

Dizemos que um espaço amostral S (finito) é equiprovável quando seus eventos elementares têm probabilidades iguais de ocorrência. Num espaço amostral equiprovável S (finito), a probabilidade de ocorrência de um evento A é sempre:

Propriedades importantes:

1. Se A e A’ são eventos complementares, então:

P(A) + P(A') = 1

2. A probabilidade de um evento é sempre um número entre 0 (probabilidade de evento impossível) e 1 (probabilidade do evento certo).