📄 Zeros ou raízes
📄 Coordenadas do vértice da parábola
📄 Construção da parábola
📄 Sinal da função
Sinal da função quadrática
Considere uma função quadrática y = f(x) = ax2 + bx + c. Vamos determinar os valores de x para os quais y é negativo e os valores de x para os quais y é positivo.
Conforme o sinal do discriminante ![]() = b2 - 4ac, podemos ocorrer os seguintes casos:
= b2 - 4ac, podemos ocorrer os seguintes casos:
1º - ![]() > 0
> 0
Nesse caso a função quadrática admite dois zeros reais
distintos (x1 ![]() x2). A parábola intercepta o eixo Ox em dois pontos e o sinal da
função é o indicado nos gráficos abaixo:
x2). A parábola intercepta o eixo Ox em dois pontos e o sinal da
função é o indicado nos gráficos abaixo:
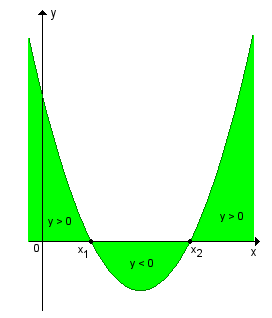
| quando a > 0 |
y > 0 ![]() (x
< x1 ou x > x2)
(x
< x1 ou x > x2)
y < 0 ![]() x1 < x < x2
x1 < x < x2
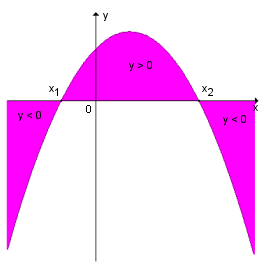
| quando a < 0 |
y > 0 ![]() x1 < x < x2
x1 < x < x2
y < 0 ![]() (x < x1 ou x > x2)
(x < x1 ou x > x2)
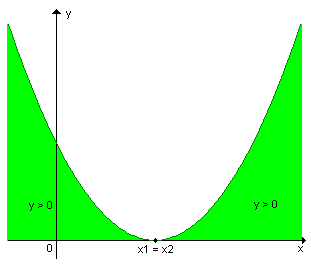
| quando a > 0 |
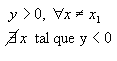
|
quando a < 0 |
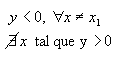
3º
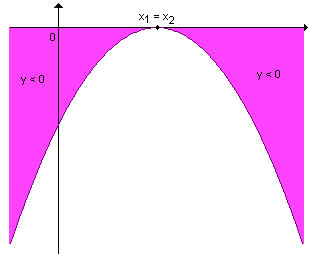
- ![]() < 0
< 0
| quando a > 0 |
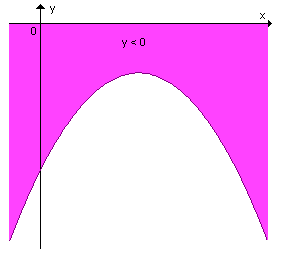
quando a < 0 |
![]()




























