|
Funções
Logarítmica e Exponencial
DERIVADAS DE FUNÇÕES LOGARÍTMICAS E EXPONENCIAIS
Agora obteremos fórmulas das derivadas para as
funções logarítmicas e exponenciais e discutiremos as relações gerais entre
e derivada de uma função um a um e a sua inversa.
- DERIVADAS DE FUNÇÕES LOGARÍTMICAS
O logaritmo natural desempenha um papel especial no cálculo que pode
ser motivado diferenciando  ,
onde b é uma base arbitrária. Para esta
proposta, admitiremos que
é
diferenciável, e portanto contínua para x > 0. Também
necessitaremos do limite
Usando a definição de derivada, obtemos(com x em vez de v
como variável).
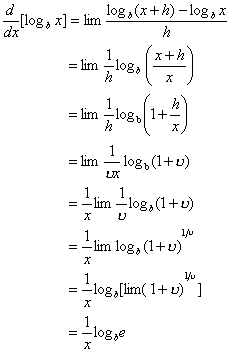
Assim,
Mas a partir da fórmula , temos 
= 1/1n b; logo, podemos
reescrever esta fórmula de derivada como
No caso especial onde b = e, temos
= 1n e = 1, logo
esta fórmula torna-se
Assim, entre todas as possíveis bases, a base b = e produz a
fórmula mais simples da derivada para
. Esta é uma das
razões por que a função do logaritmo natural é preferida sobre todos
os logaritmos no cálculo.
Exemplo 1
Ache 
Solução. A
partir de 
Quando possível as propriedades dos logaritmos devem
ser usadas para converter produtos, quocientes e expoentes em somas, em
diferenças e em múltiplos de constantes, antes de diferenciar uma função
envolvendo logaritmos.
Exemplo 2
<<
Voltar para Ensino Superior
|
