|
Funções
Logarítmica e Exponencial
Em geral, não é necessário resolver uma equação de
y em termos de x, a fim de diferenciar as funções definidas pela
equação. Para ilustrar isto, consideremos a equação
xy =
1
Uma maneira de achar dy/dx é reescrever
esta equação como
da qual tem-se que
Contudo, há uma outra maneira de obter esta derivada.
Podemos diferenciar ambos os lados de xy = 1 antes de resolver para y em
termos de x, tratando y como (não-especificado temporariamente) uma função
diferenciável de x. Com esta abordagem, obtemos
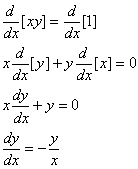
Se agora substituirmos na última
expressão, obtemos
que está de acordo com
. Este método para obter
derivadas é chamado de diferenciação implícita.
Exemplo 1
Use a diferenciação implícita para achar dy/dx
se 
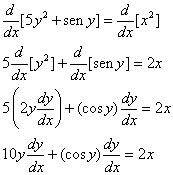
Resolvendo para dy/dx obtemos
Note que esta fórmula envolve ambos x e y.
A fim de obter uma fórmula para dy/dx que envolva apenas x,
teríamos que resolver a equação original para y em termos de x e, então,
substituir em
. Entretanto, isto é impossível de ser feito; assim,
somos forçados a deixar a fórmula dy/dx em termos de x e y.
Exemplo 2
Use a diferenciação implícita para
achar  se  .
Solução.
Diferenciado ambos os lados
de
implicitamente, obtém-se
de que obtemos
Diferenciando ambos os lados
de
implicitamente, obtém-se
Substituindo dentro de e
simplificando, usando a equação original, obtemos
Nos Exemplos 1 e 2, os resultados das fórmulas para dy/dx
envolvem ambos x e y. Embora seja usualmente mais desejável ter a fórmula
para dy/dx expressa somente em termos de x, ter a fórmula em
termos de x e y não é um impedimento para achar as inclinações e as
equações das retas tangentes, desde que as coordenadas x e y do ponto de
tangência sejam conhecidas.
<<
Voltar para Ensino Superior
|
