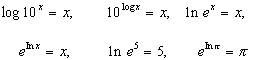📄 Domínio e imagem das funções inversas
📄 Gráficos das funções inversas
📄 Funções logarítmica e exponencial
📄 Logaritmos
📄 Funções logarítmicas
📄 Funções definidas explicitamente e implicitamente
📄 Diferenciação implícita
📄 Derivadas de potências racionais de x
📄 Derivadas de funções logarítmicas
📄 Diferenciação logarítmica
📄 Derivadas de funções exponenciais
📄 Derivadas das funções trigonométricas inversas
Funções logarítmicas
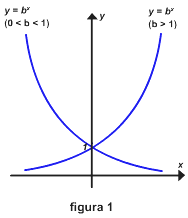
A figura 1 abaixo sugere que se b > 0 e b ![]() 1,
então o gráfico de y =
1,
então o gráfico de y = ![]() satisfaz o teste da reta horizontal, e isso implica que a função f (x)
=
satisfaz o teste da reta horizontal, e isso implica que a função f (x)
= ![]() tem uma inversa.
tem uma inversa.
Para encontrar uma fórmula para esta inversa (com x
como variável independente), podemos resolver a equação x
= ![]() para y com uma função de x. Isto pode ser feito
tomando o logaritmo na base de b de ambos os lados desta equação. Isto
dá lugar a
para y com uma função de x. Isto pode ser feito
tomando o logaritmo na base de b de ambos os lados desta equação. Isto
dá lugar a
![]() =
=
![]() (
(![]() )
)
Porém, se pensarmos ![]() (
(![]() ) como expoente ao qual b se deve
ser elevado para produzir
) como expoente ao qual b se deve
ser elevado para produzir ![]() , então fica evidente que
, então fica evidente que
![]() (
(![]() ).
Assim, pode ser reescrito como
).
Assim, pode ser reescrito como
y = ![]()
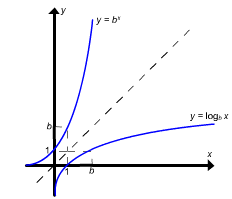
de onde concluímos que a inversa de f (x) = ![]() é
é ![]() (x) =
(x) = ![]() x. Isto implica que o
gráfico de x =
x. Isto implica que o
gráfico de x = ![]() e o de y =
e o de y = ![]() são
reflexões um do outro, em relação relação à reta y = x.
são
reflexões um do outro, em relação relação à reta y = x.
Chamaremos ![]() de
função logarítmica na base b.
de
função logarítmica na base b.
Em particular, se tomarmos f (x) = ![]() e
e ![]() (x) =
(x) = ![]() ,
e
se tivermos em mente que o domínio de
,
e
se tivermos em mente que o domínio de ![]() é o mesmo que a imagem de f,
então obtemos
é o mesmo que a imagem de f,
então obtemos
| logb(bx)=x para todos os valores reais de x blog x=x para x>0 |
Em outras palavras, a equação nos diz que as funções logb(bx) e blog x cancelam o efeito de outra quando compostas em qualquer ordem; por exemplo