Origem dos números irracionais

A origem histórica da necessidade de criação dos números irracionais está intimamente ligada com fatos de natureza geométrica e de natureza aritemética. Os de natureza geométrica podem ser ilustrados com o problema da medida da diagonal do quadrado quando a comparamos com o seu lado.

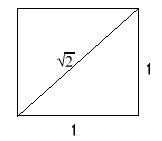
Este problema geométrico arrasta outro de natureza aritmética, que consiste na impossibilidade de encontrar números conhecidos - racionais - para raízes quadradas de outros números, como por exemplo, raiz quadrada de 2.

Estes problemas já eram conhecidos da Escola Pitagórica (séc. V a.c.), que considerava os irracionais heréticos. A Ciência grega consegui um aprofundamento de toda a teoria dos números racionais, por via geométrica - "Elementos de Euclides" - mas não avançou, por razões essencialmente filosóficas, no campo do conceito de número.

Para os gregos, toda a figura geométrica era formada por um número finito de pontos, sendo estes concebidos como minúsculos corpúsculos - "as mónadas" - todos iguais entre si; daí resultava que, ao medir um comprimento de n mónadas com outro de m, essa medida seria sempre representada por uma razão entre dois inteiros n/m (número racional); tal comprimento incluía-se, então na categoria dos comensuráveis.

Ao encontrar os irracionais, aos quais não conseguem dar forma de fracção, os matemáticos gregos são levados a conceber grandezas incomensuráveis. A reta onde se marcavam todos os racionais era, para eles, perfeitamente contínua; admitir os irracionais era imaginála cheia de "buracos". É no séc. XVII, com a criação da Geometria Analítica (Fermat e Descartes), que se estabelece a simbiose do geométrico com o algébrico, favorecendo o tratamento aritemético do comensurável e do incomensurável. Newton (1642-1727) define pela primeira vez "número", tanto racional como irracional.

O irracional ø

ø =1,6180339887... ou ø =(1 + sqr(5))/2 é considerado símbolo de harmonia. Os artistas gregos usavam-no em arquitetura; Leonardo da Vinci, nos seus trabalhos artísticos; e, no mundo moderno, o arquiteto Le Corbusier, com base nele, apresentou, em 1948, O modulor. O número de ouro descobre-se em relações métricas:

- na natureza: em animais (como na concha do Nautilus) flores, frutos, na disposição dos ramos de certas árvores;
- em figuras geométricas, tais como o retângulo de ouro, hexágono e decágono regulares e poliedros regulares;
- em inúmeros monumentos, desde a Pirâmide de Quéops até diversas catedrais, na escultura, pintura e até na música.