Você está em Ensino fundamental > Semelhança de Polígonos ▼
Propriedades da semelhança de polígonos
Se dois polígonos são
semelhantes, então a razão entre seus perímetros é igual
à razão entre as medidas de dois lados homólogos quaisquer dos
polígonos.
Demonstração:
Sendo ABCD ~ A'B'C'D', temos que:
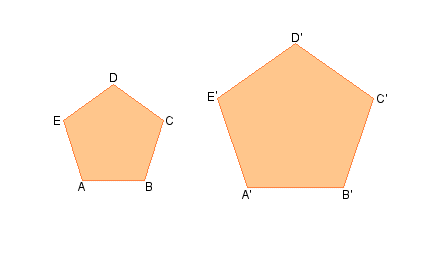
Os perímetros desses polígonos
podem ser assim representados:
Perímetro de ABCDE (2p) = AB + BC + CD +
DE + EA
Perímetro de A'B'C'D'E'
(2p') = A'B' + B'C' + C'D'
+ D'E' + E'A'
Por uma propriedade das proporções, podemos afirmar que:
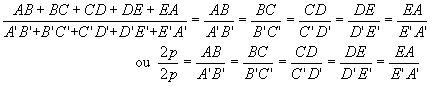
Exemplo:
-
Os lados de um triângulo medem 3,6 cm, 6,4 cm e 8 cm. Esse triângulo é semelhante a um outro cujo perímetro mede 45 cm. Calcule os lados do segundo triângulo.
Solução:
Razão de semelhança =
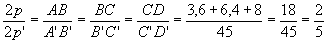
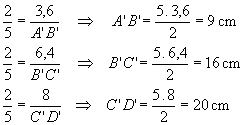
Logo, os lados do segundo triângulo são 9cm, 16cm e 20cm.
Próximo conteúdo: Operações com números racionais decimais
Como referenciar: "Semelhança de Polígonos" em Só Matemática. Virtuous Tecnologia da Informação, 1998-2024. Consultado em 22/11/2024 às 21:58. Disponível na Internet em https://www.somatematica.com.br/fundam/semelhanca/semelhanca3.php
