Função crescente ou decrescente

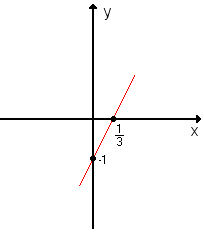
Consideremos a função do 1º grau y=3x-1. Vamos atribuir valores cada vez maiores a x e observar o que ocorre com y:

Regra geral:

- a função do 1º grau f(x) = ax + b é crescente quando o coeficiente de x é positivo (a > 0);
- a função do 1º grau f(x) = ax + b é decrescente quando o coeficiente de x é negativo (a < 0);

Justificativa:

• para a > 0: se x₁ < x₂, então ax₁ < ax₂. Daí, ax₁ + b < ax₂ + b, de onde vem f(x₁) < f(x₂).
• para a < 0: se x₁ < x₂, então ax₁ > ax₂. Daí, ax₁ + b > ax₂ + b, de onde vem f(x₁) > f(x₂).