Conceitos de conjuntos

Conjunto vazio

É um conjunto que não possui elementos. O conjunto vazio é representado por { } ou .

Subconjuntos

Quando todos os elementos de um conjunto A qualquer pertencem a um outro conjunto B, diz-se, então, que A é um subconjunto de B, ou seja AB. Observações:

• Todo o conjunto A é subconjunto dele próprio, ou seja ;
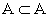• O conjunto vazio, por convenção, é subconjunto de qualquer conjunto, ou seja

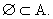
União de Conjuntos

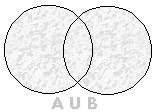
Dados os conjuntos A e B, define-se como união dos conjuntos A e B ao conjunto representado por , formado por todos os elementos pertencentes a A ou B, ou seja:

Intersecção de Conjuntos

Dados os conjuntos A e B, define-se como intersecção dos conjuntos A e B ao conjunto representado por , formado por todos os elementos pertencentes a A e B, simultaneamente, ou seja:

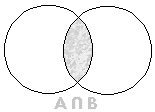
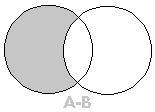
Diferença de Conjuntos

Dados os conjuntos A e B, define-se como diferença entre A e B (nesta ordem) ao conjunto representado por A-B, formado por todos os elementos pertencentes a A, mas que não pertencem a B, ou seja

Produto Cartesiano

Dados os conjuntos A e B, chama-se produto cartesiano A com B, ao conjunto AxB, formado por todos os pares ordenados (x,y), onde x é elemento de A e y é elemento de B, ou seja

Número de subconjuntos de um conjunto: se um conjunto A possuir n elementos, então existirão 2ⁿ subconjuntos de A.