EQUAÇÕES DIOFANTINAS IV – O PRINCÍPIO DA BOA ORDEM
Pierre de Fermat estabeleceu uma forma de indução denominada de "Método da Descida Infinita". Esse método é utilizado quando queremos demonstrar que certas equações diofantinas não possuem solução. Pierre de Fermat demonstrou o caso n = 4 do último teorema (UTF) de Fermat. No método da descida infinita assumimos a existência de uma solução inteira e positiva e, a partir dela, mostramos que podemos obter outra solução de valor inteiro e positivo menor que a anterior. Prosseguindo dessa maneira, construímos uma seqüência infinita decrescente de valores positivos. Contudo o Princípio da Boa Ordem afirma que todo conjunto não-vazio de números naturais possui um menor elemento e, assim, chegamos a uma contradição. Essa contradição decorre da suposição de que o problema possui uma solução inteira e positiva e assim pelo método da redução ao absurdo concluímos que o problema original não possui solução.
Utilizando o método da descida
infinita observamos que 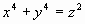 não possui solução inteira distinta da
trivial, (x, y, z), onde x.y.z ≠ 0 e z>0.
não possui solução inteira distinta da
trivial, (x, y, z), onde x.y.z ≠ 0 e z>0.
Suponhamos que os inteiros
positivos x =x0, y =y0, z =z0 são uma solução de
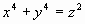 com x0 e y0 primos entre si. Observe que
com x0 e y0 primos entre si. Observe que 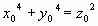 implica que
implica que 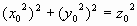 , ou seja,
, ou seja,
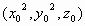 é uma Terna Pitagórica. Por outro lado, FIG. 10 e FIG.11 são primos entre
si pois, se existisse um primo p que dividisse
é uma Terna Pitagórica. Por outro lado, FIG. 10 e FIG.11 são primos entre
si pois, se existisse um primo p que dividisse 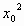 e
e 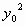 , então p
dividiria x0 e y0, contrariando o fato de que x0
e y0 são
primos entre si. Portanto,
, então p
dividiria x0 e y0, contrariando o fato de que x0
e y0 são
primos entre si. Portanto, 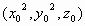 é uma Terna Pitagórica Primitiva. A partir
desta Terna Pitagórica Primitiva construímos uma nova Terna Pitagórica
Primitiva (
é uma Terna Pitagórica Primitiva. A partir
desta Terna Pitagórica Primitiva construímos uma nova Terna Pitagórica
Primitiva (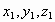 ) tal que
) tal que
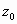 >
> 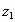 . Novamente, a partir da Terna
Pitagórica Primitiva (
. Novamente, a partir da Terna
Pitagórica Primitiva (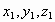 ) construímos uma outra Terna Pitagórica
Primitiva (
) construímos uma outra Terna Pitagórica
Primitiva (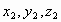 ) tal que
) tal que
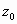 >
> 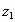 >
> 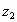 . Esse processo
pode ser repetido indefinidamente produzindo uma sequência decrescente infinita
de inteiros positivos
. Esse processo
pode ser repetido indefinidamente produzindo uma sequência decrescente infinita
de inteiros positivos 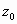 >
> 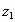 >
> 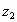 .
Pelo Princípio
da Boa Ordem, uma contradição ocorre. Portanto, somos forçados a concluir que
.
Pelo Princípio
da Boa Ordem, uma contradição ocorre. Portanto, somos forçados a concluir que
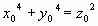 não admite solução no conjunto dos números inteiros e positivos.
não admite solução no conjunto dos números inteiros e positivos.
Como corolário imediato obtemos
que a equação 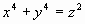 não admite solução no conjunto dos números inteiros e
positivos. De fato, se (
não admite solução no conjunto dos números inteiros e
positivos. De fato, se (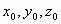 ) fosse uma solução inteira e positiva da equação
) fosse uma solução inteira e positiva da equação
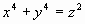 , então (
, então (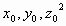 ) seria solução inteira e positiva da equação
) seria solução inteira e positiva da equação
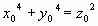 contrariando os argumentos anteriores. Assim, o último teorema de Fermat (UTF)
para o caso n = 4 é verdadeiro.
contrariando os argumentos anteriores. Assim, o último teorema de Fermat (UTF)
para o caso n = 4 é verdadeiro.




























