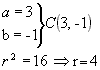Geometria Analítica: Circunferência
   

Determinação do centro e do raio da circunferência, dada a equação geral

   Dada a equação geral de uma circunferência, utilizamos o processo de fatoração de trinômio quadrado perfeito para transformá-la na equação reduzida e , assim, determinamos o centro e o raio da circunferência.

   Para tanto, a equação geral deve obedecer a duas condições:

• os coeficientes dos termos x² e y² devem ser iguais a 1;

• não deve existir o termo xy.

   Então, vamos determinar o centro e o raio da circunferência cuja equação geral é x² + y² - 6x + 2y - 6 = 0.

   Observando a equação, vemos que ela obedece às duas condições. Assim:

• 1º passo: agrupamos os termos em x e os termos em y e isolamos o termo independente

x² - 6x + _ + y² + 2y + _ = 6

• 2º passo: determinamos os termos que completam os quadrados perfeitos nas variáveis x e y, somando a ambos os membros as parcelas correspondentes

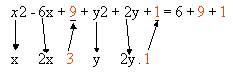
• 3º passo: fatoramos os trinômios quadrados perfeitos

( x - 3 ) ² + ( y + 1 ) ² = 16

• 4º passo: obtida a equação reduzida, determinamos o centro e o raio

Posição de um ponto em relação a uma circunferência

   Em relação à circunferência de equação ( x - a )² + ( y - b )² = r², o ponto P(m, n) pode ocupar as seguintes posições:

a) P é exterior à circunferência
b) P pertence à circunferência
c) P é interior à circunferência

    Assim, para determinar a posição de um ponto P(m, n) em relação a uma circunferência, basta substituir as coordenadas de P na expressão ( x - a )² + ( y - b )² - r²:

• se ( m - a)² + ( n - b)² - r² > 0, então P é exterior à circunferência;
• se ( m - a)² + ( n - b)² - r² =    0, então P pertence à circunferência;
• se ( m - a)² + ( n - b)² - r² < 0, então P é interior à circunferência.
     

<< Voltar para seção Ensino médio