Integrais trigonométricas

Integração de potências de seno e co-seno

Na seção fórmulas de redução, obtivemos as fórmulas:

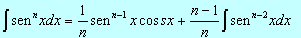
No caso onde n=2, estas fórmulas ficam:

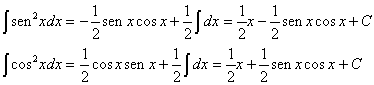
Podem-se obter formas alternativas para estas fórmulas de integração usando as identidades trigonométricas.   

que provêm das fórmulas para o ângulo duplo

Essas identidades dão lugar a

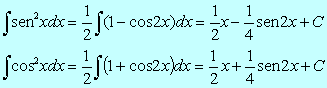
Integração de produtos de senos e co-senos

Se m e n são inteiros positivos,então a integral

pode ser calculada de diversas maneiras,dependendo de m e n serem pares ou ímpares.

Exemplo

Calcule

Solução.

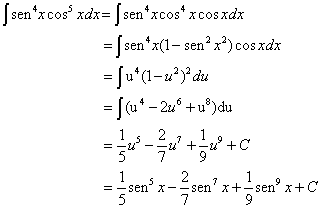
Integração de potências de tangente e de secante

O procedimento para integração de potências de tangente e de secante segue paralelamente os do seno e co-seno. A ideia é usar as seguintes fórmulas de redução para reduzir o expoente do integrando até que a integral resultante possa ser calculada:

No caso onde n for ímpar,o expoente pode ser reduzido a um,nos deixando com o problema de integrar tg x ou sec x.Estas integrais são dadas por

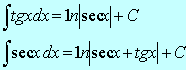
A fórmula pode ser obtida escrevendo-se

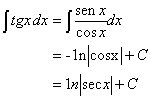
A fórmula requer um truque.Escrevemos

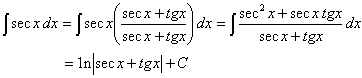
As seguintes integrais ocorrem freqüentemente,e vale a pena destacar:

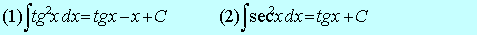
A fórmula(2)já foi vista,uma vez que a derivada de tgx é  .A fórmula(1) pode ser obtida aplicando-se a fórmula de redução,com n=2,ou alternativamente,usando-se a identidade

para escrever