Integrais

Integrais indefinidas

Da mesma forma que a adição e a subtração, a multiplicação e a divisão, a operação inversa da derivação é a antiderivação ou integração indefinida.

Dada uma função g(x), qualquer função f'(x) tal que f'(x) = g(x) é chamada integral indefinida ou antiderivada de f(x).

Exemplos:

1. Se  f(x) = 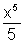, então 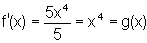é a derivada de f(x). Uma das antiderivadas de f'(x) = g(x) = x⁴ é .
      
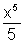2. Se f(x) = x³, então f'(x) = 3x² = g(x). Uma das antiderivadas ou integrais indefinidas de g(x) = 3x² é f(x) = x³.
      
3. Se f(x) = x³ + 4, então f'(x) = 3x² = g(x). Uma das antiderivadas ou integrais indefinidas de g(x) = 3x² é f(x) = x³ + 4.

Nos exemplos 2 e 3 podemos observar que tanto x³ quando x³+4 são integrais indefinidas para 3x². A diferença entre quaisquer destas funções (chamadas funções primitivas) é sempre uma constante, ou seja, a integral indefinida de 3x² é x³+C, onde C é uma constante real.

Propriedades das integrais indefinidas

  São imediatas as seguintes propriedades:

1ª.    , ou seja, a integral da soma ou diferença é a soma ou diferença das integrais.

2ª.   , ou seja, a constante multiplicativa pode ser retirada do integrando.

3ª.    , ou seja, a derivada da integral de uma função é a própria função.

Integração por substituição

Seja expressão . 

Através da substituição u=f(x) por u' = f'(x) ou , ou ainda, du = f'(x) dx, vem:

,

admitindo que se conhece .

O método da substituição de variável exige a identificação de u e u' ou u e du na integral dada.