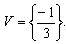Resolução de uma equação

Resolver uma equação consiste em realizar uma série de operações que nos conduzem a equações equivalentes cada vez mais simples, que nos permitem determinar os elementos do conjunto verdade ou as raízes da equação. Resumindo:

Na resolução de uma equação do 1º grau com uma incógnita, devemos aplicar os princípios de equivalência das igualdades (aditivo e multiplicativo). Exemplos:

• Sendo 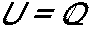  , resolva a equação    .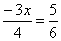

MMC (4, 6) = 12

-9x = 10  =>   Multiplicador por (-1)

9x = -10

Como  , então .

• Sendo 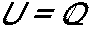, resolva a equação 2.(x - 2) - 3.(1 - x) = 2.(x - 4).

Iniciamos aplicando a propriedade distributiva da multiplicação:

2x - 4 - 3 + 3x = 2x - 8 

2x + 3x -2x = - 8 + 4 + 3

3x = -1

Com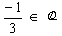o  , então