Você está em Ensino médio > Geometria analítica - Retas ▼
📄 Introdução
📄 Plano cartesiano
📄 Distância entre dois pontos
📄 Razão de secção
📄 Ponto médio
📄 Baricentro de um triângulo
📄 Condições de alinhamento de três pontos
📄 Equação geral
📄 Equação segmentária
📄 Equações paramétricas
📄 Equação reduzida
📄 Coeficiente angular
📄 Representação gráfica de retas
📄 Posições relativas entre retas
📄 Ângulo entre duas retas
📄 Distância entre ponto e reta
📄 Bissetrizes
📄 Plano cartesiano
📄 Distância entre dois pontos
📄 Razão de secção
📄 Ponto médio
📄 Baricentro de um triângulo
📄 Condições de alinhamento de três pontos
📄 Equação geral
📄 Equação segmentária
📄 Equações paramétricas
📄 Equação reduzida
📄 Coeficiente angular
📄 Representação gráfica de retas
📄 Posições relativas entre retas
📄 Ângulo entre duas retas
📄 Distância entre ponto e reta
📄 Bissetrizes
Ponto médio
Dados
os pontos A(xA, yA), B(xB, yB)
e P, que divide 
ao meio, temos:
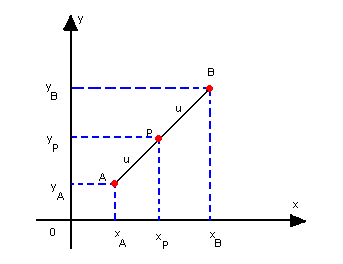
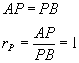
Assim:
Logo, as coordenadas do ponto médio são dadas por:
Próximo: Baricentro de um triângulo
Como referenciar: "Geometria analítica - Retas" em Só Matemática. Virtuous Tecnologia da Informação, 1998-2024. Consultado em 21/11/2024 às 09:23. Disponível na Internet em https://www.somatematica.com.br/emedio/retas/retas3.php
