Gráfico de uma equação de 1º grau com duas variáveis

Sabemos que uma equação do 1º grau com duas variáveis possui infinitas soluções. Cada uma dessas soluções pode ser representada por um par ordenado (x, y).

Dispondo de dois pares ordenados de um equação, podemos representá-los graficamente em um plano cartesiano, determinando, através da reta que os une, o conjunto das soluções dessa equação. Exemplo:

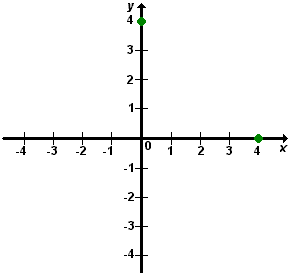
• Construir um gráfico da equação x + y  = 4.

Inicialmente, escolhemos dois pares ordenados que solucionam essa equação.

  1º par: A (4, 0)

  2º par: B (0, 4)

A seguir, representamos esses pontos em um plano cartesiano.

Finalmente, unimos os pontos A e B, determinando a reta r, que contém todos os pontos soluções da equação.

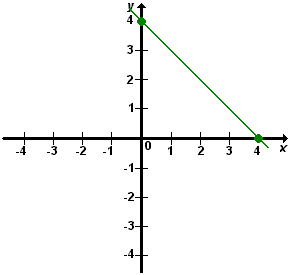A reta r é chamada reta suporte do gráfico da equação.