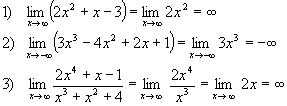Limites envolvendo infinito

Conforme sabemos, a expressão:

x (x tende para infinito)

significa que x assume valores superiores a qualquer número real e x (x tende para menos infinitos), da mesma forma, indica que x assume valores menores que qualquer número real.

Exemplo:

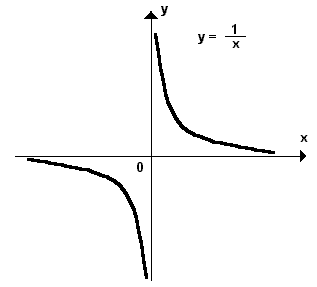
a) , ou seja, à medida que x aumenta,  y tende para zero e o limite é zero.

b) , ou seja, à medida que x diminui,  y tende para zero e o limite é zero. 

c) , ou seja, quando  x se aproxima de zero pela direita de zero ou por valores maiores que zero, y tende para o infinito e o limite é infinito.

d) , ou seja, quando x  tende para zero pela esquerda ou por valores menores que zero, y tende para menos infinito

Limite de uma função polinomial para

Seja a função polinomial . Então:

Demonstração:

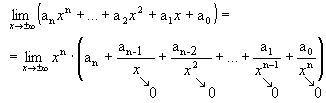
Mas:

Logo:

De forma análoga, para , temos:

Exemplos: