Distribuição normal

A distribuição normal é a mas importante distribuição estatística, considerando a questão prática e teórica.

Já vimos que esse tipo de distribuição apresenta-se em formato de sino, unimodal, simétrica em relação a sua média.

Considerando a probabilidade de ocorrência, a área sob sua curva soma 100%. Isso quer dizer que a probabilidade de uma observação assumir um valor entre dois pontos quaisquer é igual à área compreendida entre esses dois pontos.

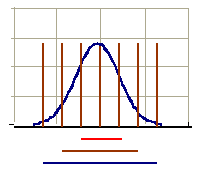
68,26% => 1 desvio
95,44% => 2 desvios
99,73% => 3 desvios

Na figura acima, tem as barras na cor marrom representando os desvios padrões. Quanto mais afastado do centro da curva normal, mais área compreendida abaixo da curva haverá. A um desvio padrão, temos 68,26% das observações contidas. A dois desvios padrões, possuímos 95,44% dos dados comprendidos e finalmente a três desvios, temos 99,73%. Podemos concluir que quanto maior a variablidade dos dados em relação à média, maior a probabilidade de encontrarmos o valor que buscamos embaixo da normal.

Propriedade 1

f(x) é simétrica em relação à origem, x = média = 0.

Propriedade 2

f(x) possui um máximo para z=0, e nesse caso sua ordenada vale 0,39.

Propriedade3

f(x) tende a zero quando x tende para + infinito ou - infinito.

Propriedade 4

f(x) tem dois pontos de inflexão cujas abscissas valem média + DP e média - DP, ou quando z tem dois pontos de inflexão cujas abscissas valem +1 e -1.

Para se obter a probabilidade sob a curva normal, utilizamos a tabela de faixa central.

Clique aqui para ver o exemplo 8