Sistemas lineares

Equação linear

Equação linear é toda equação da forma:

a₁x₁ + a₂x₂+ a₃x₃ + ... + a_nx_n = b

em que a₁, a₂, a₃, ... , a_n são números reais, que recebem o nome de coeficientes das incógnitas x₁, x₂,x₃, ... , x_n, e b é um número real chamado termo independente (quando b=0, a equação recebe o nome de linear homogênea).

Veja alguns exemplos de equações lineares:

3x - 2y + 4z = 7

-2x + 4z = 3t - y + 4

(homogênea)

As equações a seguir não são lineares:

xy - 3z + t = 8

x²- 4y = 3t - 4

Sistema linear

Um conjunto de equações lineares da forma:

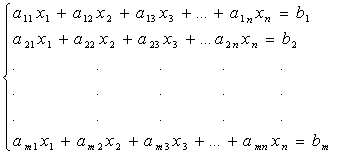
é um sistema linear de m equações e n incógnitas.

A solução de um sistema linear é a n-upla de números reais ordenados (r₁, r₂, r₃,..., r_n) que é, simultaneamente, solução de todas as equações do sistema.