Você está em Ensino superior > Equações diferenciais ▼
📄 Definição e classificação
📄 Equações lineares homogêneas, 2ª ordem
📄 Equações diferenciais lineares de ordem N
📄 Equações lineares homogêneas, 2ª ordem
📄 Equações diferenciais lineares de ordem N
Equações lineares homogêneas, 2ª ordem
FORMA : y'' + a1y' + a0y = 0 (a0, a1 constantes)
Ex: y = ![]()
Então y' = ![]()
![]() e y'' =
e y'' = ![]()
![]()
Substituindo na equação dada:
![]()
ou
![]() (
(![]() ) = 0
) = 0
![]()
![]() 0 para todo x, logo devemos ter
0 para todo x, logo devemos ter ![]() = 0, que é uma equação do segundo grau na variável
= 0, que é uma equação do segundo grau na variável ![]() , chamada equação característica.
, chamada equação característica.
A solução da equação diferencial linear irá depender da raízes ![]() 1 e
1 e ![]() 2.
2.
-
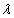 1,
1, 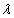 2 números reais e distintos
2 números reais e distintos 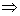 C1
C1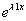 e C2
e C2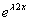 são soluções particulares da EDO e a solução geral é y = C1
são soluções particulares da EDO e a solução geral é y = C1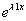 + C2
+ C2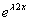
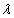 1 =
1 = 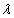 2 =
2 = 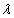 (números reais e iguais)
(números reais e iguais) 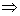 a solução geral da EDO é y = C1
a solução geral da EDO é y = C1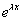 + C2x
+ C2x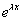
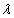 1 = a + bi,
1 = a + bi, 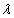 2 = a - bi (complexos conjugados: a, b reais)
2 = a - bi (complexos conjugados: a, b reais) 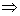 a solução geral é y = C1
a solução geral é y = C1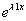 + C2
+ C2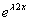
Ex: y'' - 2y' - 15y = 0
Equação característica: ![]() - 2
- 2![]() - 15 = 0 cujas raízes são:
- 15 = 0 cujas raízes são: ![]() 1 = 5,
1 = 5, ![]() 2= -3
2= -3
Solução geral: y = ![]()
Como referenciar: "Equações diferenciais" em Só Matemática. Virtuous Tecnologia da Informação, 1998-2026. Consultado em 05/02/2026 às 03:17. Disponível na Internet em https://www.somatematica.com.br/superior/equacoesdif/eq2.php




























