Como interpretar problemas matemáticos

Você sabia que o português está diretamente ligado à resolução de problemas matemáticos? Exatamente! Se você não souber interpretar o enunciado de uma questão, fica difícil converter as informações do problema para linguagem matemática.

Pensando nisso, o Só Matemática preparou algumas dicas para ajudar você a interpretar certas informações que são comuns nos enunciados das questões de concursos, vestibulares ou até daquela simples tarefa de casa.

Qual é o número...?

Provavelmente você já deve ter visto a pergunta acima. Quando ela aparece, significa que precisamos encontrar o valor de um número, então vamos logo chamá-lo de x. Portanto, já escreva:

x = ?

Aliás, sempre que aparecerem perguntas envolvendo pronomes interrogativos (como "qual" e "quanto"), significa que precisamos encontrar o x da questão.

E quando aparecem as preposições?

Fique atento quando encontrar preposições como "de", "da" e "do", pois elas costumam indicar uma operação de multiplicação.

Por exemplo, se um problema pede de x, temos a expressão:

, que equivale a .

Veja outro caso:

Lucas tem 21 anos. Quanto vale da sua idade?
(veja que usamos a multiplicação)

Acompanhe mais um exemplo:

Quanto vale ?

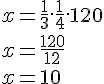
Outra preposição que aparece bastante nos problemas matemáticos é a "por", que normalmente indica uma operação de divisão. Repare que essa preposição também está "escondida" dentro do sinal % ("por cento"). Veja os exemplos:

2 por 3 =

Quanto vale 1/5 de 10% de 500?

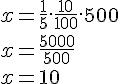
O dobro, o triplo, a metade...

Você também poderá encontrar as palavras abaixo, que são traduzidas da seguinte forma na matemática.

O dobro de um n°? 2x

O triplo de um n°? 3x

O quádruplo de um n°? 4x

A metade de um nº?

A terça parte de um nº?

A quarta parte de um nº?

E assim por diante.

Verbos

No enunciado da questão, verbos como "é", "tem" e "equivale" significam igualdade. Acompanhe os enunciados a seguir e suas traduções para linguagem matemática.

Carlos e João têm juntos 50 anos.
C + J = 50

Rodrigo tem 10 anos a mais que Marcelo.
R = M + 10

Daqui a 5 anos, a idade de Luiz será a metade da idade de Pedro.

Repare que, na hora de formar a equação, ao somarmos cinco anos na idade de Luiz, devemos somar também 5 anos na idade de Pedro, pois o tempo passa da mesma forma para ambos.

O dobro de um número aumentado em 6 equivale à quinta parte deste número diminuído de 7.

Observe agora essas duas perguntas, que parecem ser iguais, porém possuem uma diferença:

Qual é a metade de cinco mais cinco?
Qual é a metade de: cinco mais cinco?

A quebra da frase causada pelos dois pontos (:) indica que devemos calcular primeiro a expressão que vem depois deste sinal (5+5), para depois encontrar sua metade. Já na primeira frase, onde não há pausas, lendo da esquerda para direita, calculamos primeiro a metade de 5, para depois somar os outros 5. Resumindo, as duas expressões seriam:

Qual a metade de cinco mais cinco?

Qual a metade de: cinco mais cinco?

Soma, diferença, produto e quociente

Estes termos indicam, respectivamente, o reultado das operações de adição, subtração, multiplicação e divisão. Portanto:

Soma de x e y significa: x+y

Diferença entre a e b significa: a-b

Produto de x e y significa: x.y ou xy

Quociente entre a e b significa:

Veja alguns exemplos de expressões:

O quádruplo da soma de a e b:
4.(a+b)

A oitava parte da diferença de x e y:

Antecessor e consecutivo

São outros termos bem frequentes nas questões matemáticas:

O antecessor de um número significa x-1
O consecutivo de um número significa x+1

Repare como é importante analisar bem o enunciado da questão. Essas suas expressões são totalmente diferentes:

O triplo do consecutivo de um número
O consecutivo do triplo de um número

A primeira representa a expressão matemática 3(x+1), enquanto a segunda representa a expressão 3x+1.

Caso o enunciado apresente a expressão "dois números consecutivos", você pode representá-los como:
x e x+1

Da mesma forma, se forem três números consecutivos, teríamos:
x, x+1 e x+2

Oposto e inverso

Por fim, você pode encontrar também os seguintes termos:

Oposto de um número significa -x
Inverso de um número significa

Por exemplo:

O oposto do inverso de um número é igual a 5.

Gostou deste artigo? Aguarde, em breve teremos mais dicas de outros assuntos!

<< Voltar para Dúvidas Frequentes